ヒープソート

ソートのアルゴリズムのうち高速なアルゴリズムとして知られているヒープソートについて解説する

１．ヒープ

大きさ9の配列を考えよう。Fig.1のように値が保存されているものとする。

Fig.1 配列表現

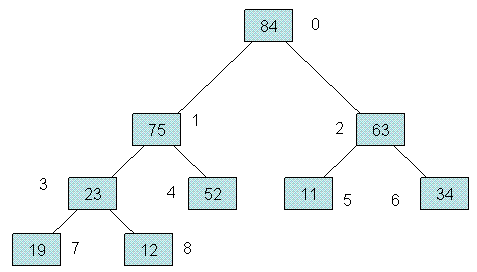
この配列要素をFig.2のように配置し，線で結んだものを考える。

Fig.2 二分木表現

各要素を示している四角い箱のことを「ノード」という。各ノードは斜め下向きの2つの線で結んだ2つのノードを持つ。（下に配置されたノードでは，下位のノードを１つしか持たない場合もあり，まったく持たない場合もある。）
このように表現されたものを「二分木」と呼ぶ。

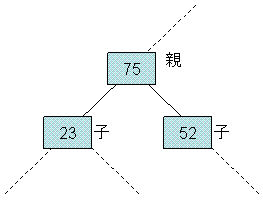
線で結ばれた3つのノードのグループのうち，上にあるノードを「親」，下にあるノードを「子」と呼ぶ。特に二分木の一番上のノードは「ルート（根）」と呼ばれる。ルートから順に図のように，要素に番号をつけると，それはノード番号となる。（Fig.2では0〜8）

Fig.3 親ノードと子ノード

二分木の場合，ノード番号n の親は (n - 1) / 2，子は 2n + 1 と 2n + 2 である（整数型の割り算では，小数点以下は切り捨てられる）。
次のようなマクロ関数を用意しておくと便利である

便利なマクロ関数

#define LeftChild(n) (2*(n)+1)
#define RightChild(n) (2*(n)+2)
#define Parent(n) (((n)-1)>>1)

図の二分木では，子同士の値の大小関係は決まっていないが，親と子の間では，親の値の方が子の値より大きくなっている（等しいこともある。）。このように，親子の間だけに値の大小関係がある木構造のことを，「半順序木（ヒープ）」と読んでいる。

２．ヒープソート

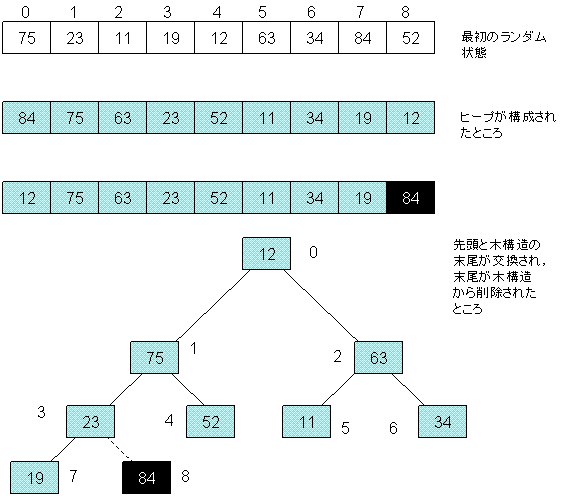
ヒープソートはこの半順序木を用いたソートの手法で，次のように行われる。

（１）ソートを求められたデータについて何らかの方法で半順序木（ヒープ）を構成する。
（２）0番要素（根）と最終要素を交換し，最終要素を木構造から切り離す。
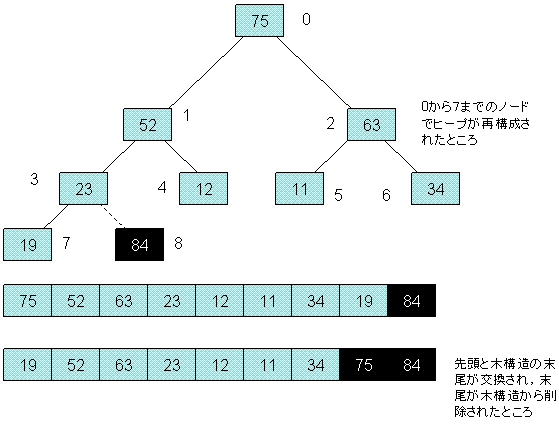
（３）半順序木（ヒープ）が壊れたので（ルートのところだけが壊れている），再構築する。
（４）「（２）」へ戻り，「（２），（３）」を木構造がなくなるまで繰り返す。

ヒープソート実行の最初の様子をFig.4，Fig.5に示す。

Fig.4 ヒープソート（１）
半順序木（ヒープ）を構成し，先頭と木構造の末尾を交換し，末尾を木構造から削除したところ

Fig.5 ヒープソート（２）
半順序木（ヒープ）を再構成し，先頭と木構造の末尾を交換し，末尾を木構造から削除したところ

プログラミングでは，最初の「半順序木（ヒープ）」構成作業と「半順序木（ヒープ）」再構成作業の2つの関数を作成するところが主な仕事となる。

３．半順序木（ヒープ）の構成

「半順序木」になっていない配列の状態から開始し，0番要素から順に「半順序木」に登録する。
0番目要素は無条件に登録されますが，2番目以降の要素は，親要素と大きさ比較し，必要なら親要素と子要素を交換する。交換したら，親要素がルートでない限り，親要素はそのまた親要素と比較して，必要なら親要素と子要素を交換する。

List.1 ヒープ構成関数　x:ヒープを構成したい配列，num:配列の大きさ

void heapify(int x[], int num)
{
    int i,child,parent,tmp;
    for (i=0; i<num; i++) {
        child=i;
        while (child) {
            parent=Parent(child);
            if (x[parent]<x[child]) {
                tmp=x[parent];
                x[parent]=x[child];
                x[child]=tmp;
                child=parent;
            } else {
                child=0; /*抜け出すため*/
            }
        }
    }
}

４．半順序木（ヒープ）の再構成

ルートの値のみ半順序木の定義を満たしていない状態（親のほうが小さい）を修正して，半順序木を作りたい。
ルートから始めて，その2つの子の大きい方と親とを比較して，親のほうが大きかったら交換する。
交換したら，子のそのまた子についても比較交換し，子がなくなるまで繰り返すことになる。

ヒープ再構成関数　x:ヒープを構成したい配列，num:配列の大きさ

void shiftDown(int x[], int num)
{
    int parent,leftchild,rightchild,t,tmp;
    parent=0;
    leftchild=LeftChild(parent);
    rightchild=RightChild(parent);
    while (leftchild<num) {
        t=leftchild;
        if (rightchild<num && x[leftchild]<x[rightchild]) t=rightchild;
        if (x[parent]<x[t]) {
            tmp=x[parent];
            x[parent]=x[t];
            x[t]=tmp;
            parent=t;
            leftchild=LeftChild(parent);
            rightchild=RightChild(parent);
        } else {
            leftchild=num;
        }
    }
}

５．ヒープソートプログラム例

ヒープソートプログラム例

/*ノードの番号を次のようにつける
       0
    1        2
3    4     5     6
7 8 9 10 11 12 13 14
親をnとすると左の子は2*n+1，右の子は2n+2
子をnとすると親は(n-1)>>1

#include "stdio.h"
#include "stdlib.h"

#define DEBUG
#define DEBUG2

#ifdef DEBUG
#define SIZE 20
#else
#define SIZE 100000
#endif

void makedata(int x[], int num)
{
int i;
for (i=0; i<num; i++) x[i]=rand()%(5*SIZE);
}

void printdata(int x[], int num)
{
    int i;
    for (i=0; i<num; i++) printf("%2d ",x[i]);
    printf("\n");
}

#ifdef DEBUG2
void printdata2(int x[], int num)
{
    int i;
    printf("=>");
    for (i=0; i<num; i++) printf("%2d ",x[i]);
    printf("\n");
}
#endif

/*小さい順ソート済みデータのチェック
　　返す値０：正常
　　　　　１：異常あり
*/
int checkSortedData(int x[], int num)
{
    int i;
    int ng=0;
    for (i=0; i<num-1; i++) {
        if (x[i+1]<x[i]) {
            printf("%2d %2d\n",x[i],x[i+1]);
            ng=1;
        }
    }
    return ng;
}

#define LeftChild(n) (2*(n)+1)
#define RightChild(n) (2*(n)+2)
#define Parent(n) (((n)-1)>>1)

void heapify(int x[], int num)
{
    int i,child,parent,tmp;
    for (i=0; i<num; i++) {
        child=i;
        while (child) {
            parent=Parent(child);
            if (x[parent]<x[child]) {
                tmp=x[parent];
                x[parent]=x[child];
                x[child]=tmp;
                child=parent;
            } else {
                child=0;
            }
        }
    }
}

void shiftDown(int x[], int num)
{
    int parent,leftchild,rightchild,t,tmp;
    parent=0;
    leftchild=LeftChild(parent);
    rightchild=RightChild(parent);
    while (leftchild<num) {
        t=leftchild;
        if (rightchild<num && x[leftchild]<x[rightchild]) t=rightchild;
        if (x[parent]<x[t]) {
            tmp=x[parent];
            x[parent]=x[t];
            x[t]=tmp;
            parent=t;
            leftchild=LeftChild(parent);
            rightchild=RightChild(parent);
        } else {
            leftchild=num;
        }
    }
}

void HeapSort(int x[], int num)
{
    int i,tmp;
    heapify(x,num);
    for (i=num-1; 0<i; i--) {
        tmp=x[i];
        x[i]=x[0];
        x[0]=tmp;
        shiftDown(x,i);
#ifdef DEBUG2
        printdata2(x, num);
#endif
    }
}

#ifdef DEBUG
int main()
{
    static int x[SIZE];
    int ng,i;
    for (i=0;i<10;i++) {
        makedata(x,SIZE);
        printdata(x,SIZE);
        HeapSort(x,SIZE);
        printdata(x,SIZE);
        ng=checkSortedData(x,SIZE);
        if (ng) printf("no good\n");
        printf("\n");
    }
    return 0;
}
#else
int main()
{
    static int x[SIZE];
    int ng;
    int i;
    for (i=0; i<100; i++) {
        makedata(x,SIZE);
        HeapSort(x,SIZE);
        ng=checkSortedData(x,SIZE);
        if (ng) printf("no good\n");
        else printf("good\n");
    }
    return 0;
}
#endif

実行例の一部

41 67 34 0 69 24 78 58 62 64 5 45 81 27 61 91 95 42 27 36
=>91 81 78 67 64 69 61 62 58 41 5 24 45 27 34 0 36 42 27 95
=>81 67 78 62 64 69 61 36 58 41 5 24 45 27 34 0 27 42 91 95
=>78 67 69 62 64 45 61 36 58 41 5 24 42 27 34 0 27 81 91 95
=>69 67 61 62 64 45 34 36 58 41 5 24 42 27 27 0 78 81 91 95
=>67 64 61 62 41 45 34 36 58 0 5 24 42 27 27 69 78 81 91 95
=>64 62 61 58 41 45 34 36 27 0 5 24 42 27 67 69 78 81 91 95
=>62 58 61 36 41 45 34 27 27 0 5 24 42 64 67 69 78 81 91 95
=>61 58 45 36 41 42 34 27 27 0 5 24 62 64 67 69 78 81 91 95
=>58 41 45 36 24 42 34 27 27 0 5 61 62 64 67 69 78 81 91 95
=>45 41 42 36 24 5 34 27 27 0 58 61 62 64 67 69 78 81 91 95
=>42 41 34 36 24 5 0 27 27 45 58 61 62 64 67 69 78 81 91 95
=>41 36 34 27 24 5 0 27 42 45 58 61 62 64 67 69 78 81 91 95
=>36 27 34 27 24 5 0 41 42 45 58 61 62 64 67 69 78 81 91 95
=>34 27 5 27 24 0 36 41 42 45 58 61 62 64 67 69 78 81 91 95
=>27 27 5 0 24 34 36 41 42 45 58 61 62 64 67 69 78 81 91 95
=>27 24 5 0 27 34 36 41 42 45 58 61 62 64 67 69 78 81 91 95
=>24 0 5 27 27 34 36 41 42 45 58 61 62 64 67 69 78 81 91 95
=> 5 0 24 27 27 34 36 41 42 45 58 61 62 64 67 69 78 81 91 95
=> 0 5 24 27 27 34 36 41 42 45 58 61 62 64 67 69 78 81 91 95
0 5 24 27 27 34 36 41 42 45 58 61 62 64 67 69 78 81 91 95