マージソート

高速ソートの一種であるマージソートについて解説する。

１．マージソート

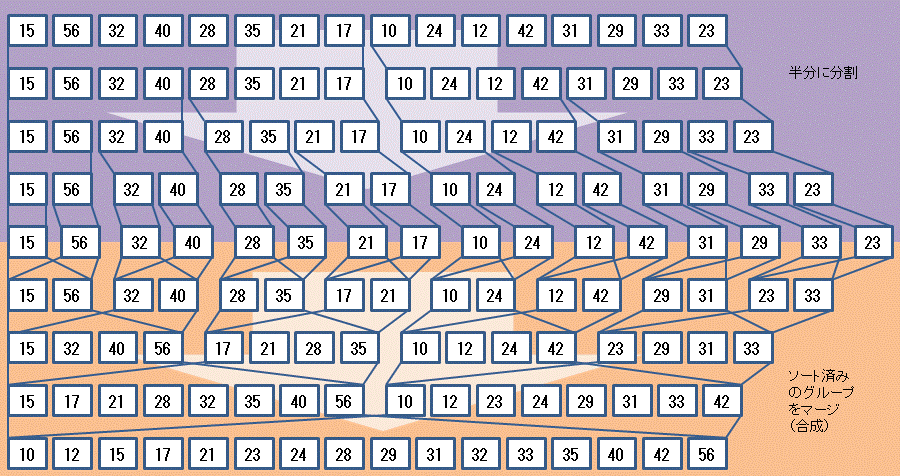
次の一連の図は「マージソート」により，昇順ソートをしているところを模式的に示している。
マージ（merge）とは，併合・吸収のことであり，マージソートでいうところのマージとは，すでにソートが完了されている２つのデータ列をまとめて1つのデータ列にすることを意味している。
ソート手順の前半は分割し，要素数1つになるまで分割する。後半ではマージを繰り返し，全体がソートされた状態にまで到達する。

２．マージソートの関数プログラム

プログラムでは，再帰を用いて実現する。ソート対象の配列を2つに分けて昇順ソートしてもらい，その後，ソートされているはずの2つの配列を1つにマージする。

要素数nの配列x[]を対象としたマージソート本体の関数を次に示す。
ただし，ソート済みの2つの配列を1つにマージする作業は別の関数としている。
この関数では，配列要素数が1以下で呼び出された時は何もしないようになっているので，要素数を半分に減らしながらの再帰呼び出しが無限呼び出しにならないことが保証される。

List 1 要素数nの配列x[]について，マージソートを行う関数
x[]:挿入ソート対象配列
num:配列要素数

void _mergesort(int x[], int num)
{
    int n1,n2;
    if (num<=1) return;
    n2=num>>1;
    n1=num-n2;
    _mergesort(&x[0],n1); /*要素番号0から始まる前半（要素数n1）のソート*/
    _mergesort(&x[n1],n2); /*要素番号n1から始まる後半（要素数n2）のソート*/
    _merge(x,n1,n2);       /*配列xの前半n1個と後半n2個がそれぞれソート済となっているので*/
                           /*１つのソートされた配列になるようにマージ*/
}

３．マージのプログラミング例

「２」で示した「マージ」，すなわちソート済みの2つの配列を1つにマージする作業を行う方法はいくつかあるが，２つの例を示す。

（１）半領域退避法

マージの際には作業領域を必要とするが，この方法では，最大で，ソート対象配列要素数の半分の長さの作業領域配列を必要とする。マージしたい配列（常に作業対象配列の前半と後半はソート済の２つの配列とみなしている）の後半部分を作業領域に退避させ，前半部分と作業領域のそれぞれの後ろから，大きい方を取り出して，元の配列の後ろから埋めてゆく手順を取る。

図でA→Bでは後半を作業領域に移動しているところである。
図でB→Cでは，前半部分と作業領域のそれぞれの後ろから，大きい方を取り出して，元の配列の後ろから埋めているところである。

半領域退避法の関数を次に示す。２つの配列は，1つの配列の前半n個と後半m個の要素で構成されている。

List 2 ソート済みの2つの配列を1つにマージする作業を行う関数　（半領域退避法）
x[]:対象配列
n:前半配列の要素数　すなわち要素番号0からn-1までが前半要素
m:後半配列の要素数　すなわち要素番号nからm-1までが後半要素
                    すなわち，この配列は要素番号0からn+m-1までで出来ている

void _merge(int x[], int n, int m)
{
    int i,j,k;
    for (i=n,j=0; j<m; i++,j++) _work[j]=x[i]; /*x[]の後半の要素を作業領域にコピー*/
    i=n-1;
    j=m-1;
    k=n+m-1;
    while ( -1<j && -1<i ) {
        if (x[i]<=_work[j]) x[k--]=_work[j--];
        else               x[k--]=x[i--];
    }
    while (-1<j) x[k--]=_work[j--];
}

（２）全領域退避法

マージの際には作業領域を必要とするが，この方法では，最大で，ソート対象配列要素数と同じの長さの作業領域配列を必要とする。マージしたい配列（常に作業対象配列の前半と後半はソート済の２つの配列とみなしている）の前半を作業領域の前半にそのままコピーし，マージしたい配列の後半を作業領域の後半に，逆順にコピーする。その後，作業領域の前半は前から，作業領域の後半は後ろから，小さい方を取り出して，元の配列の前から埋めてゆく手順を取る。この手順によれば，元の配列に書き戻す際に，作業領域は番兵法を使っているのと同じ状態になり，終端チェックが不要で高速に作業を進めることができるとされている。ただし，半領域退避法に比べて，最初に２倍のコピー作業があり，このことは動作を遅くさせている。
どちらが早いか比べてみるよよい。

図でA→Bでは前半・後半を作業領域に移動しているところである。ただし，後半は逆順になっている。
図でB→Cでは，作業領域前半部分は前から，作業領域後半部分は後ろから，小さい方を取り出して，元の配列の前から埋めているところである。

全領域退避法の関数を次に示す。２つの配列は，1つの配列の前半n個と後半m個の要素で構成されている。

List 3 ソート済みの2つの配列を1つにマージする作業を行う関数　（全領域退避法）
x[]:対象配列
n:前半配列の要素数　すなわち要素番号0からn-1までが前半要素
m:後半配列の要素数　すなわち要素番号nからm-1までが後半要素
                    すなわち，この配列は要素番号0からn+m-1までで出来ている

void _merge(int x[], int n, int m)
{
    int i,j,k;
    for (i=0; i<n; i++) _work[i]=x[i];
    for (j=n+m-1; n<=j; j--) _work[i++]=x[j];
    i=0;
    j=n+m-1;
    k=0;
    while ( i<=j ) {
        if (_work[i]<=_work[j]) x[k++]=_work[i++];
        else                   x[k++]=_work[j--];
    }
}

４．マージソートのプログラミング例

マージソート関数を用いたプログラミング例を次に示す。マージ関数は２つあるので関数_mergesort()中でどちらか片方を呼び出せばよい。また作業領域は動的に確保している。マージソートの時にmainが呼び出すのは，関数mergesort()のみであり，「_」で始まる関数や_workはmainは手を出さないように使ってもらう。

List 4 シェルソートプログラミング例

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define SIZE 100

int data[SIZE];

void printData(int x[], int num)
{
    int i;
#if 1000<SIZE
    return;
#endif
    for (i=0; i<num; i++) {
        printf("%6d",x[i]);
        if (i%10==9) printf("\n");
    }
}

void generateData(int x[], int num)
{
    int i;
    for (i=0; i<num; i++) x[i]=rand();
}

int *_work;
/*x[]の前半n個と後半m個のデータをマージする*/
/*前半と後半はそれぞれ，昇順にソートされているものとする*/
void _merge0(int x[], int n, int m)
{
    int i,j,k;
    for (i=n,j=0; j<m; i++,j++) _work[j]=x[i];
    i=n-1;
    j=m-1;
    k=n+m-1;
    while ( -1<j && -1<i ) {
        if (x[i]<=_work[j]) x[k--]=_work[j--];
        else               x[k--]=x[i--];
    }
    while (-1<j) x[k--]=_work[j--];
}

void _merge1(int x[], int n, int m)
{
    int i,j,k;
    for (i=0; i<n; i++) _work[i]=x[i];
    for (j=n+m-1; n<=j; j--) _work[i++]=x[j];
    i=0;
    j=n+m-1;
    k=0;
    while ( i<=j ) {
        if (_work[i]<=_work[j]) x[k++]=_work[i++];
        else                   x[k++]=_work[j--];
    }
}

void _mergesort(int x[], int num)
{
    int n1,n2;
    if (num<=1) return;
    n2=num>>1;
    n1=num-n2;
    _mergesort(&x[0],n1);
    _mergesort(&x[n1],n2);
    _merge0(x,n1,n2);     /*半領域退避法　この２つのうちどちらかを用いる*/
    //_merge1(x,n1,n2);   /*全領域退避法　この２つのうちどちらかを用いる*/
}

void mergesort(int x[], int num)
{
    _work=(int *)malloc(num*sizeof(int));
    _mergesort(x,num);
    free(_work);
}

int main()
{
    srand((unsigned) time(NULL)); /*乱数列生成の初期化*/
    generateData(data,SIZE);
    printf("befor sort\n");
    printData(data,SIZE);
    printf("\n");
    mergesort(data,SIZE);
    printf("after sort\n");
    printData(data,SIZE);
    printf("\n");
    return 0;
}