シェルソート

Donald L. Shellが開発したソートのアルゴリズムである。高速ソートの一種であるシェルソートについて解説する

１．シェルソート

次の一連の図は「4→2→1シェルソート」により，昇順ソートをしているところを模式的に示している。

１．ソート前の状態

２．最初は「4-ソート」といって，4つずつ離れたデータのグループごとに，昇順挿入ソートを行っている。「4-ソート」が終わってもグループごとにソートされているだけなので，全体としてソートされるわけではない。

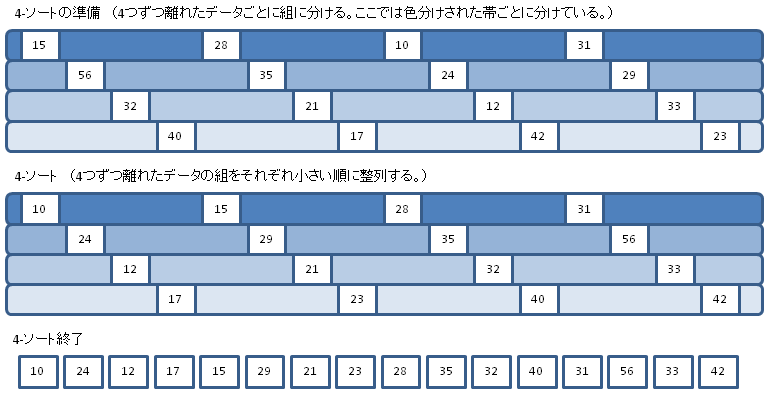
３．次は「2-ソート」といって，２つずつ離れたデータのグループごとに，昇順挿入ソートを行っている。「2-ソート」が終わってもグループごとにソートされているだけなので，全体としてソートされるわけではない。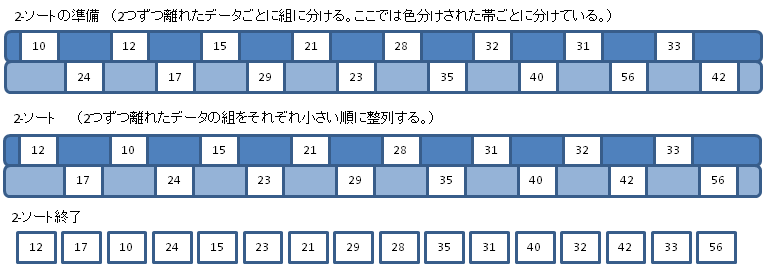

４．最後は「1-ソート」といって，全体を1グループとして昇順挿入ソートを行う。すでにかなり大小関係によって分布が偏っているので，昇順挿入ソートを実行しても，移動手数は少なくてすむはずである。

このように，いくつかのグループに分けて，予備的にソートを行い，だいたいソートを終わらせて，最後に手直し的なソートを行うようにするのが，シェルソートである。どの回のソートにおいても，移動量はそれほど大きくはならないのが，このソートの高速さの理由である。

ここに示したソートは，４，２，１ソートの順で行ったが，倍数にならない数列によるソートの方が，効率がよい。さまざまな数列が用いられるが，最後は１で終わるようにしなければならない。よく用いられるのは１から始めて，3倍して１を加える数列（１，４，１３，４０，１２１，・・・）を逆にたどる数列である。ただし，要素数の１／９以下で構成される数列がよいとされている。

ここで示したソートを，実行するプログラムは複数の実現方法が考えられる。4重ループで実現するプログラムと3重ループで実現するプログラムの2つを紹介する。また原理通りに行っているプログラムと，番兵法を用いてさらに高速化したプログラムも紹介する。

２．シェルソートのプログラミング例１　（4重ループで実現）

最初に模式図をそのまま実現する方法を示す。要素数nの配列x[]について，先頭要素番号headで始まるgapごと離れた要素グループに対して挿入ソートを行う関数を作っておく。例えばgap=4でheadは0,1,2,3の4つを行うと「１」に示した「4-ソート」を実行したことになる。すなわち「k-ソート」では，gap=kとし，head=0からgap-1まで変化させながらループさせることになる。そしてこの「headに関するループ」について，gapを数列に従って減少変化させながらgap=1になるまでループさせる2重ループになる。

次に示すのが要素数nの配列x[]について，先頭要素番号headで始まるgapごと離れた要素グループに対して挿入ソートを行う関数である。通常の挿入ソートを手直しして作ることができる。

List 1 要素数nの配列x[]について，先頭要素番号headで始まるgapごと離れた要素グループに対して挿入ソートを行う関数
x:挿入ソート対象配列の先頭アドレス
num:配列要素数
head:グループの先頭番号
gap:グループを構成する要素の間隔

void gapinsertionsort(int x[], int num, int head, int gap)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int blank; /*隙間要素の番号*/
    int tmp;   /*退避場所*/
    for (i=head+gap; i<num; i+=gap) {
        tmp=x[i]; /*着目要素の退避*/
        j=i;
        /*tmpと比較して右移動させるかどうか検討する要素はx[j-gap]*/
        while (tmp<x[j-gap] && 0<=j-gap) {
            x[j]=x[j-gap];
            j-=gap;
        }
        x[j]=tmp;
    }
}

もし，番兵法を導入して，改良を加えると次のようになる。

List 2 要素数nの配列x[]について，先頭要素番号headで始まるgapごと離れた要素グループに対して挿入ソートを行う関数
番兵法を用いた方法
x:挿入ソート対象配列の先頭アドレス
num:配列要素数
head:グループの先頭番号
gap:グループを構成する要素の間隔

void gapinsertionsort_withSentinel2(int x[], int num, int head, int gap)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*退避場所*/
    for (i=head+gap; i<num; i+=gap) {
        tmp=x[head]; /*グループの先頭要素を退避*/
        x[head]=x[i]; /*挿入対象の値をグループの先頭要素にする*/
        j=i;
        /*x[head]と比較して右移動させるかどうか検討する要素はx[j-gap]*/
        while (x[head]<x[j-gap]) {
            x[j]=x[j-gap];
            j-=gap;
        }
        if (x[head]<=tmp) {
            x[j]=tmp;
        } else {
            x[j]=x[head];
            x[head]=tmp;
        }
    }
}

List 1，list 2の挿入ソートを呼び出すのが，シェルソート本体となる。
最初にgapの数列を１から順に作り，num/9を超える前で止める。gapを３で割りながら，1<=gapの範囲で繰り返しを行う。
このループの内部で，先頭要素番号を表すheadを0からhead<gapまで繰り返している。

List 3 シェルソート関数
x:シェルソート対象配列の先頭アドレス
num:配列要素数

void shellsort_mainloop(int x[], int num)
{
    int gap=1;
    int head;
    while (gap<num/9) gap=gap*3+1;
    while (1<=gap) {
        for (head=0; head<gap; head++) {
            gapinsertionsort_withSentinel2(x, num, head, gap);
        }
        gap/=3;
    }
}

３．シェルソートのプログラミング例２　（3重ループで実現）

「２」で示したシェルソートは４重ループになっていた。ここではよくつかわれている３重ループで記述する方法を取り上げるが，移動の手間は４重ループプログラムとほとんど変わらない。
３重ループのうち，内側の２重ループは，挿入ソートと同様だが，挿入ソートが隣同士の比較により，要素を移動していたところを，gap離れた要素同士の比較により，要素を移動しているところが異なるところである。最外側のループはgapを数列に従って変化させている。
この記述でも，「１」に示したグループごとのソートの実行が確保されていることがわかる。

List 4 シェルソート
x:シェルソート対象配列の先頭アドレス
num:配列要素数

void shellsort(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*退避場所*/
    int gap=1;   /*グループを作る要素間隔*/
    while (gap<num/9) gap=gap*3+1;
    for ( ;1<=gap ;gap/=3) {
        for (i=gap; i<num; i++) {
            tmp=x[i]; /*着目要素の退避*/
            j=i;
            /*tmpと比較して右移動させるかどうか検討する要素はx[j-gap]*/
            while ( 0<=j-gap && tmp<x[j-gap] ) {
                x[j]=x[j-gap];
                j-=gap;
            }
            x[j]=tmp;
        }
    }
}

シェルソートに対しても番兵法を適用できる。しかし，毎回，グループの先頭要素番号を計算する必要があるため，４重ループ記述の方がスマートかもしれない。

List 5 シェルソート関数　番兵法
x:シェルソート対象配列の先頭アドレス
num:配列要素数

void shellsort_withSentinel2(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*先頭要素の退避場所*/
    int gap=1; /*グループを作る要素間隔*/
    int head; /*各グループの先頭要素番号*/
    while (gap<num/9) gap=gap*3+1;
    for ( ;1<=gap ;gap/=3) {
        for (i=gap, head=0; i<num; i++) {
            tmp=x[head]; /*グループの先頭要素を退避*/
          x[head]=x[i]; /*挿入対象の値をグループの先頭要素にする*/
            j=i;
            /*x[head]と比較して右移動させるかどうか検討する要素はx[j-gap]*/
            while (x[head]<x[j-gap]) {
                x[j]=x[j-gap];
                j-=gap;
            }
            if (x[head]<=tmp) {
                x[j]=tmp;
            } else {
                x[j]=x[head];
                x[head]=tmp;
            }
            if (++head==gap) head=0;
        }
    }
}

４．シェルソートのプログラミング例

シェルソート関数を用いたプログラミング例を次に示す。挿入ソートも参考のため残してある。
main中のソート関数を１つだけ残すようにすればよい。

List 4 シェルソートプログラミング例

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define SIZE 1000

int data[SIZE];

void printData(int x[], int num)
{
    int i;
#if 1000<SIZE
    return;
#endif
    for (i=0; i<num; i++) {
        printf("%6d",x[i]);
        if (i%10==9) printf("\n");
    }
}

void generateData(int x[], int num)
{
    int i;
    for (i=0; i<num; i++) x[i]=rand();
}

void insertionsort(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*退避場所*/
    for (i=1; i<num; i++) {
        tmp=x[i]; /*着目要素の退避*/
        j=i;
        /*tmpと比較して右移動させるかどうか検討する要素はx[j-1]*/
        while ( 0<j && tmp<x[j-1] ) {
            x[j]=x[j-1];
            j--;
        }
        x[j]=tmp;
    }
}

void shellsort(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*退避場所*/
    int gap=1;   /*グループを作る要素間隔*/
    while (gap<num/9) gap=gap*3+1;
    for ( ;1<=gap ;gap/=3) {
        for (i=gap; i<num; i++) {
            tmp=x[i]; /*着目要素の退避*/
            j=i;
            /*tmpと比較して右移動させるかどうか検討する要素はx[j-gap]*/
            while ( 0<=j-gap && tmp<x[j-gap] ) {
                x[j]=x[j-gap];
                j-=gap;
            }
            x[j]=tmp;
        }
    }
}

void insertionsort_withSentinel(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*先頭要素の退避場所*/
    for (i=1; i<num; i++) {
        tmp=x[0]; /*先頭要素を退避*/
        x[0]=x[i]; /*挿入対象の値を第0要素にする*/
        j=i;
        /*x[0]と比較して右移動させるかどうか検討する要素はx[j-1]*/
        while (x[0]<x[j-1]) {
            x[j]=x[j-1];
            j--;
        }
        if (j==1) { /*whileループで先頭まで到達した*/
            if (tmp<x[0]) {
                x[1]=x[0];
                x[0]=tmp;
            } else {
                x[1]=tmp;
            }
        } else { /*途中でwhileを脱出した*/
            x[j]=x[0];
            x[0]=tmp;
        }
    }
}

void shellsort_withSentinel(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*先頭要素の退避場所*/
    int gap=1; /*グループを作る要素間隔*/
    int head; /*各グループの先頭要素番号*/
    while (gap<num/9) gap=gap*3+1;
    for ( ;1<=gap ;gap/=3) {
        for (i=gap, head=0; i<num; i++) {
          tmp=x[head]; /*グループの先頭要素を退避*/
          x[head]=x[i]; /*挿入対象の値をグループの先頭要素にする*/
            j=i;
            /*x[head]と比較して右移動させるかどうか検討する要素はx[j-gap]*/
            while (x[head]<x[j-gap]) {
                x[j]=x[j-gap];
                j-=gap;
            }
            if (j==head+gap) { /*whileループで先頭まで到達した*/
                if (tmp<x[head]) {
                    x[head+gap]=x[head];
                    x[head]=tmp;
                } else {
                    x[head+gap]=tmp;
                }
            } else { /*途中でwhileを脱出した*/
                x[j]=x[head];
                x[head]=tmp;
            }
            if (++head==gap) head=0;
        }
    }
}

void insertionsort_withSentinel2(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*先頭要素の退避場所*/
    for (i=1; i<num; i++) {
        tmp=x[0]; /*先頭要素を退避*/
        x[0]=x[i]; /*挿入対象の値を第0要素にする*/
        j=i;
        /*x[0]と比較して右移動させるかどうか検討する要素はx[j-1]*/
        while (x[0]<x[j-1]) {
            x[j]=x[j-1];
            j--;
        }
        if (x[0]<=tmp) {
            x[j]=tmp;
        } else {
            x[j]=x[0];
            x[0]=tmp;
        }
    }
}

void shellsort_withSentinel2(int x[], int num)
{
    int i;     /*挿入要素の番号*/
    int j;     /*要素を退避したことによって生まれる空要素の要素番号*/
    int tmp;   /*先頭要素の退避場所*/
    int gap=1; /*グループを作る要素間隔*/
    int head; /*各グループの先頭要素番号*/
    while (gap<num/9) gap=gap*3+1;
    for ( ;1<=gap ;gap/=3) {
        for (i=gap, head=0; i<num; i++) {
            tmp=x[head]; /*グループの先頭要素を退避*/
          x[head]=x[i]; /*挿入対象の値をグループの先頭要素にする*/
            j=i;
            /*x[head]と比較して右移動させるかどうか検討する要素はx[j-gap]*/
            while (x[head]<x[j-gap]) {
                x[j]=x[j-gap];
                j-=gap;
            }
            if (x[head]<=tmp) {
                x[j]=tmp;
            } else {
                x[j]=x[head];
                x[head]=tmp;
            }
            if (++head==gap) head=0;
        }
    }
}

int main()
{
    srand((unsigned) time(NULL)); /*乱数列生成の初期化*/
    generateData(data,SIZE);
    printf("befor sort\n");
    printData(data,SIZE);
    printf("\n");
    //insertionsort(data,SIZE);
    //insertionsort_withSentinel(data,SIZE);
    //insertionsort_withSentinel2(data,SIZE);
    //shellsort(data,SIZE);
    //shellsort_withSentinel(data,SIZE);
    shellsort_withSentinel2(data,SIZE);
    printf("after sort\n");
    printData(data,SIZE);
    printf("\n");
    return 0;
}