PWM信号を使った2つの駆動方式とは次のようなものです。
〇 通電・絶縁駆動
〇 通電・ショート駆動
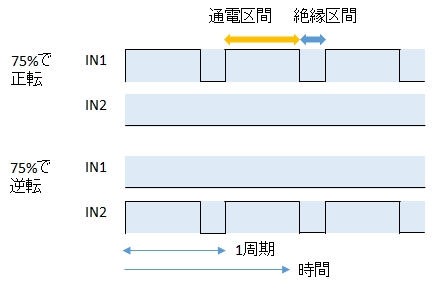
通電・絶縁駆動
例えば,デューティ比75%順方向駆動のとき,75%順方向駆動,25%停止(フリー)で動作させます。
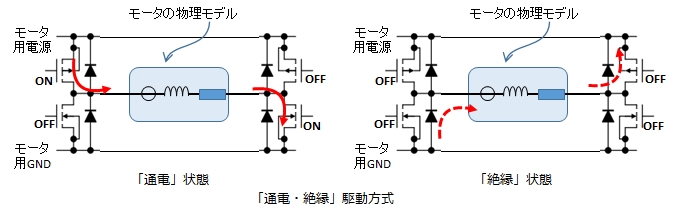
通電・ショート駆動
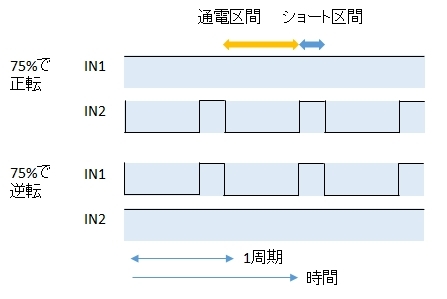
同じように,デューティ比75%順方向駆動のとき,75%順方向駆動,25%停止(ショートブレーキ)で動作させます。
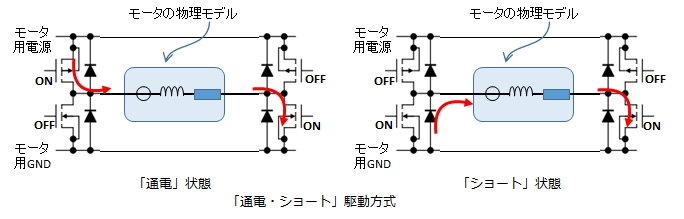
2つの駆動方式では,停止区間での電流の流れ方に違いがあります。
2023.3.2 Coskx Lab
1 はじめに
DCブラシモータをモータドライバICでPWM駆動するとき,低いデューティ比を設定したときに,モータトルクが予想より低下して,モータが回り始めないことがあると言われています。
モータトルクは電流に比例しますので,モータ停止状態で低いデューティ比を与えたときの駆動電流について考察します。
モータドライバICを使ったモータのPWM駆動では次の2つの駆動方式が主に使われます。
〇 通電・絶縁駆動
〇 通電・ショート駆動
それぞれの駆動方式において,PWM周期,デューティ比で駆動したとき,モータ停止状態での電流値がどうなるかを考察したいと思います。
・PWM(Pulse Width Modulation,パルス 幅変調)
モータドライバICで,モータを駆動するとき,高速にON-OFFを繰り返し,ONの時間とOFFの時間を調整する方法はPWM駆動と呼ばれます。
高速にON-OFFを繰り返す周期はPWM周期,1周期中のONになっている時間の割合はデューティ比と呼ばれます。
2 モータドライバICのふるまい
DCブラシモータのPWM駆動にはモータドライバICが使われますが,その2つの入力信号と,モータ駆動電流の流れは次のようになっています。
IN1,IN2の信号とモータドライバの各FETの動作は次の表のようになります。
| IN1 | IN2 | 左上 FET |
左下 FET |
右上 FET |
右下 FET |
電流状態 | モータの状態 |
|---|---|---|---|---|---|---|---|
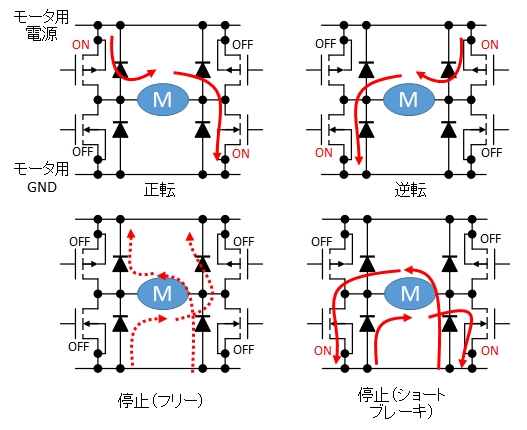
| High | Low | ON | OFF | OFF | ON | 正転通電 | 正転 |
| Low | High | OFF | ON | ON | OFF | 逆転通電 | 逆転 |
| Low | Low | OFF | OFF | OFF | OFF | 絶縁 | 停止(フリー) |
| High | High | OFF | ON | OFF | ON | ショート | 停止(ショートブレーキ) |
3 2つのPWM駆動方式
モータドライバICで,PWM駆動を実現するときには2つの駆動方式が考えられます。
PWM信号を使った2つの駆動方式とは次のようなものです。
〇 通電・絶縁駆動
〇 通電・ショート駆動
通電・絶縁駆動
例えば,デューティ比75%順方向駆動のとき,75%順方向駆動,25%停止(フリー)で動作させます。


通電・ショート駆動
同じように,デューティ比75%順方向駆動のとき,75%順方向駆動,25%停止(ショートブレーキ)で動作させます。


2つの駆動方式では,停止区間での電流の流れ方に違いがあります。
4 DCブラシモータの特性と,定電圧駆動
DCモータには,内部に巻き線があり,これはインダクタンス成分となります。この巻き線は線が細く長いため,抵抗があります。
また,モータが回転しているときは発電機として働き,逆起電力も働きます。逆起電力として発生する電圧は,モータの回転速度に比例しています。
すなわちDCモータはインダクタンス \(L\) と純抵抗 \(R\) と電圧発生器」の直列結合とみなすことが出来ます。
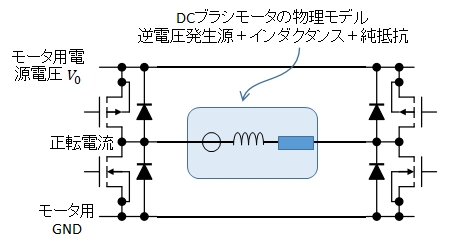
単純化のために,モータドライバの内部抵抗はないものとします。
通電時のモータモデルは次のようになっています。
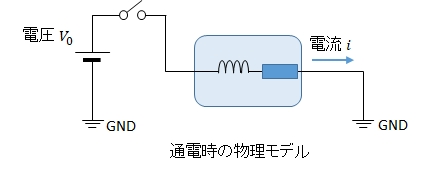
モータに加える電圧を \(v_0(t)\),モータに流れる電流を \(i(t)\),モータが発生している逆起電圧を \(v_\omega\),モータの内部抵抗を\(R\) とします。
一定角速度\(\omega\)でモータは回転しているとき,逆起電力定数(比例定数)を \(k_v\) とすると逆起電力は \(v_\omega = k_v \omega\) で表されます。
モータに流れる電流は次の式を満たします。
$$L\frac{d}{dt} i(t) + R i(t) +v_\omega = v_0(t) \tag{1}$$
\(t=0\)のときに,電流が \(i_0\) で,モータに加えられた電圧が急に一定値(電源電圧) \(V_0\) になったという条件のもとで,電流は次のように得られます。
$$i(t) = \dfrac{V_0-v_\omega}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big)+i_0 \exp(-\dfrac{1}{\tau}t) \tag{2}$$
ただし \(\tau = L / R\) で, \(\tau\) は時定数と呼ばれ,時間の単位[sec]を持っています。
特にモータが停止状態の場合は,\(v_\omega = 0\) なので
$$i(t) = \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big)+i_0 \exp(-\dfrac{1}{\tau}t) \tag{3}$$
になります。
さらに \(t=0\) のときに,電流が \(0\) であれば
$$i(t) = \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big) \tag{4}$$
になります。
十分に時間が経過したときには電流値は最大になり,
$$i(t) = \dfrac{V_0}{R} \tag{5}$$
になります。
式(4)をグラフにすると次のようになります。横軸は時間ですが,\(\tau\)の何倍かを目盛にしています。縦軸は電圧ですが式(5)の何倍かを目盛にしています。
電流値は最大値に収束することがわかります。
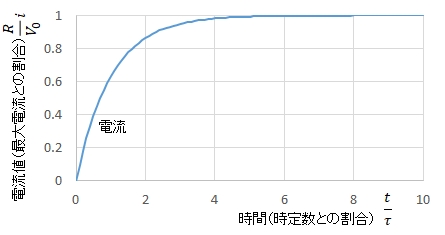
\(t=\tau\) はこのグラフで時刻が1のときのことであり,このときの電流は式(4)より
\(i(\tau)=\dfrac{V_0}{R} (1-\dfrac{1}{e})=0.632\dfrac{V_0}{R} \)
になります。
5 DCブラシモータのPWM駆動
DCモータをPWM駆動したときの電流の様子を考えます。
軸を回転できないようにし,逆起電力が発生しない状態を考えることにします。( \(v_\omega = 0\) )
PWM周期 \(T\) を \(\tau\) の \(P\) 倍で表すと,\(T=P\tau\)となります。
デューティ比を \(d\) で表します。(\(0 \leqq d \leqq 1\))
PWM駆動方法として,「3」で示した通り,「通電・絶縁駆動」と「通電・ショート駆動」の2通りがあるため,それぞれについて,電流の様子を考えてみます。
5.1 DCブラシモータのPWM駆動(通電・絶縁駆動)
通電・絶縁駆動のときは次の2つの状態を交互に繰り返します。
絶縁状態ではモータドライバの4つのFETがOFFになります。
このとき,ダイオードの作用で電流の流れる方向は制限されていますが,モータに加わる電圧は通電状態と逆向きになります。

5.1.1 電流計算
モータ軸は回転していないとします。(\(v_\omega = 0\) )
通電・絶縁駆動の1周期を通電区間・絶縁区間で別々に考えます。
〇 通電区間では,\(t=0\) から \(t = t_a = T d \) まで電圧 \(V_0\) を加えます。ただし \(d\) はデューティ比です。(\(0 \leqq d \leqq 1\))
\(0 \leqq t \leqq t_a\) の区間での電流値は式(4)で表されます。
通電区間の終了時 \(t = t_a\) の電流値を \(i_a \) で表すと
$$i_a = i_{(T d)} = \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau} T d)\Big) \tag{6}$$
となります。
〇 絶縁区間 \(t_a < t \leqq T\) では,FETはすべてOFFですが,ダイオードの働きにより,逆向きに電圧を加えている状態になりますが,電流はこれに逆らって,左下から右上に流れる点線で示した経路に流れます。
絶縁時のモータモデルは次のようになっています。
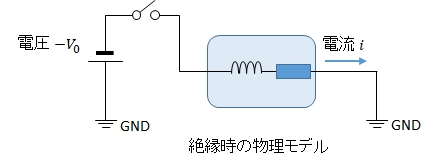
ここで絶縁区間の始まりを改めて時刻 \(0\) として考えると,電流初期値は \(i_a\) となっています。
絶縁区間の電流は式(3)で \(V_0\) を \(-V_0\) に置き換え,\(i_0\) を \(i_a\) に置き換えた次の形で表されます。
$$\begin{eqnarray}
i(t) &=& -\dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big)+i_a \exp(-\dfrac{1}{\tau}t)
\\ &=& -\dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big)+\dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau} T d)\Big) \exp(-\dfrac{1}{\tau}t)
\\ &=& \dfrac{V_0}{R} \bigl\{ -1 + \Big(2-\exp(- \dfrac{1}{\tau}Td)\Big) \exp(- \dfrac{1}{\tau}t)\bigr\}
\tag{7}
\end{eqnarray}$$
この式では電流は \(i_a\) から急速に減少します。
ただし,ダイオードの働きによって,電流値は負の値にはなりません。
式(7)では
$$\dfrac{t}{\tau} = \log \Big(2-\exp(-\dfrac{1}{\tau}Td)\Big) \tag{8}$$
で \(i(t) = 0\) になります。それ以降は式(7)は無効になり,電流は \(0\) を保ちます。
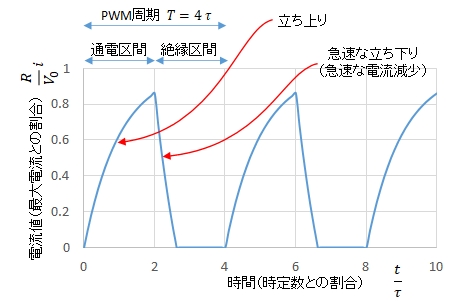
〇 例 \(P=4\) すなわちPWM周期 \(T = 4 \tau\) のとき,デューティ比 \(d=0.5\) では,電流値は次のグラフのようになります。
立ち上がり部分は式(4)であり,急速な立ち下り部分は式(7)になります。
5.1.2 電流の実測
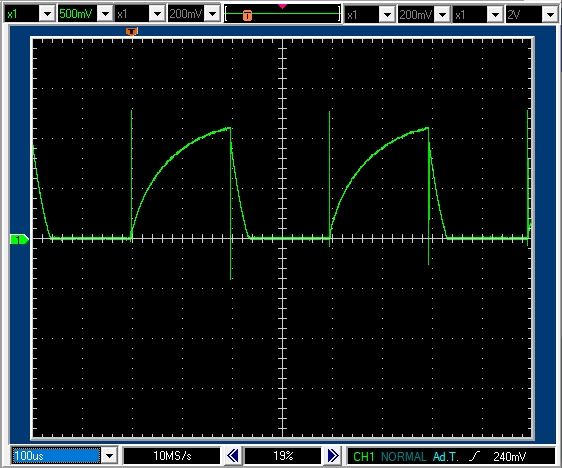
次の図は,\(P \risingdotseq 4\) すなわちPWM周期 \(T \risingdotseq 4\tau\) (実際にはPWM周期0.4msec)のとき,デューティ比 \(d=0.5\) のときの電流値を実際に測定したものです。
モータ軸は固定して,モータと直列に \(1\Omega\) の抵抗を挿入し,その両端電位差から測定しています。
絶縁区間に入った後に,急速に減衰する電流が見えますが,回路図の左下から右上に流れる点線で示した経路と考えられます。
\(T\)の測定精度はそれほど良くないので,計算値とのずれは仕方がないと考えられます。
5.1.3 平均電流の計算
平均電流値 \(i_m\) は,1周期の電流を積分して1周期の長さで割ることで求められます。
1周期の間に,通電区間の立ち上がり,絶縁区間内に高速立ち下りと電流が0の領域がありますが,デューティ比 \(d\) が1に近くなると絶縁区間が短くなり立ち下がりが絶縁区間に収まらなくなる場合があります。
ここでは,低デューティ比でのふるまいに着目するため,高速立ち下り区間長が絶縁区間長より短い場合を考えることにします。
すなわち,式(8)より
$$\tau \ \log \Big(2-\exp(-\dfrac{1}{\tau}Td)\Big) < T-d \tag{9}$$
を考えます。
積分計算は,通電区間の立ち上がり( \(I_1\) )と絶縁区間内にの高速立ち下り( \(I_2\) )を別々に計算することにします。
それぞれ,式(4)および式(7)を使い,区間の始まりを時刻 \(0\) とします。
ただし,\(P = T / \tau\) とします。
$$\begin{eqnarray}
I_1 &=& \int_{0}^{P \tau d} \Big\{ \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big) \Big\} dt \tag{10}
\\
I_2 &=& \int_{0}^{\tau \log (2 - \exp(-Pd))} \Big\{ \dfrac{V_0}{R} \bigl\{ -1 + \big(2-\exp(- Pd)\big) \exp(- \dfrac{1}{\tau}t)\bigr\} \Big\} dt \tag{11}
\end{eqnarray}$$
これを計算すると平均電流値 \(i_m\) は,次式で表されます。
$$\begin{eqnarray}
i_m &=& \dfrac{I_1 +I_2}{T}
\\
&=& \dfrac{V_0}{R} \Big\{ d - \dfrac{1}{P} \big( 1 - \exp(-P d) \big)
\\
&& + \dfrac{1}{P} \Big(1-\exp(-Pd)-\log\big(2-\exp(-Pd)\big)\Big) \Big\}
\\
&=& \dfrac{V_0}{R} \Big( d - \dfrac{\log \big(2-\exp(-Pd)\big)}{P} \Big)\tag{12}
\end{eqnarray}$$
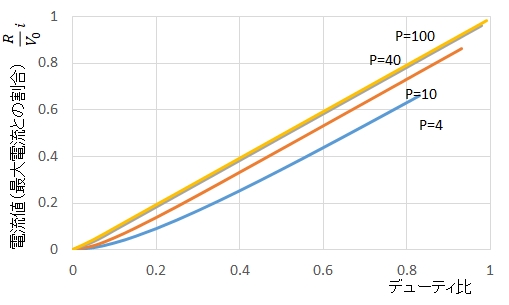
\(P = T/ \tau\) の値,すなわちPWM周期をモータの電気的時定数の何倍に設定するかの値によって,デューティ比と平均電流値がどのような関係になるかを式(12)にしたがって次のグラフに表します。
各曲線の右側が消えているのは,計算の条件(立ち下がりが絶縁区間に収まる)を満たしていない部分です。
デューティ比と平均電流値は比例している関係が望ましいのですが,\(P\) の値が10より小さいと,指定したデューティ比に対して平均電流値が小さくなることがわかります。特に,低デューティ比のときに平均電流値が小さくて,トルク不足で回転を始められない原因になっていると考えられます。
\(P\)が大きければ起動できない問題は緩和されますが,あまり大きくする( \(100 < P\) )と,モータ駆動系の機械的時定数に近づいて,ここでは触れませんが,別の問題が生ずる場合があります。
5.2 DCブラシモータのPWM駆動(通電・ショート駆動)
通電・絶縁駆動のときは次の2つの状態を交互に繰り返します。

5.2.1 電流計算
モータ軸は回転していないとします。(\(v_\omega = 0\) )
PWM駆動を開始直後の解は過渡解と呼ばれます。
PWM駆動開始後,しばらくして,定常的な状態になったときの解は定常解と呼ばれます。
[過渡解]
通電・絶縁駆動の1周期を通電区間・ショート区間を別々に考えます。
〇 通電区間では,\(t=0\) から \(t = t_1 = T d \) まで電圧 \(V_0\) を加えます。ただし \(d\) はデューティ比です。(\(0 \leqq d \leqq 1\))
\(0 \leqq t \leqq t_1\) の区間での電流値は式(4)で表されます。
通電区間の終了時 \(t = t_1\) の電流値を \(i_1 \) で表すと
$$i_1 = i_{(T d)} = \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau} T d)\Big) \tag{13}$$
になります。この値は次のショートブレーキ区間に入ったときの初期電流値になります。
〇 ショートブレーキ区間に入るので,改めてその時点を \(t=0\) として,新しい時間軸で計算を進めます。
ショート時のモータモデルは次のようになっています。
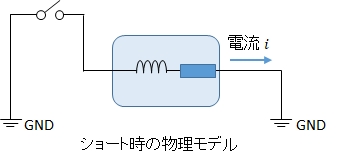
モータ軸が回転していないときの電流は式(3)で表せますが,この区間は式(3)において,電源電圧を0にしたことに対応するので, \(V_0 = 0\) とします。そして \(t = 0\) のときの電流値は \(0\) ではなく \(i_1 \) になっているので,電流は,式(3)より
$$i(t) = i_1 \exp(-\dfrac{1}{\tau}t) \tag{14}$$
で表すことができます。
ショートブレーキ区間が終わるときは新しい時間軸で \(t = Pr(1-d)\) なので,そのときの電流値を \(i_2\) で表すと
$$i_2 = i_{(Pr(1-d))} = i_1 \exp\Big(-\dfrac{1}{\tau}Pr(1-d)\Big) \tag{15}$$
になっています。この値は次の駆動区間に入ったときの初期電流値になります。
次の駆動期間に入ったら,再びその時点を \(t=0\) として,新しい時間軸で計算を進めます。
モータ軸が回転していないときの電流は式(3)で表せますが,加えられている電圧は復活し,初期電流値は \(t_2\) になっています。
電流値は
$$i(t) = \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big)+i_2 \exp(-\dfrac{1}{\tau}t) \tag{16}$$
となります。
そして再び電流値を引継ぎ,次のショートブレーキ区間に入って行きます。この後,同様のことが繰り返されます。
〇 例 \(P=4\) すなわちPWM周期 \(T = 4 \tau\) のとき,デューティ比 \(d=0.5\) では,電流値は次のグラフのようになります。
スタート時に電流は \(0\) になっています。
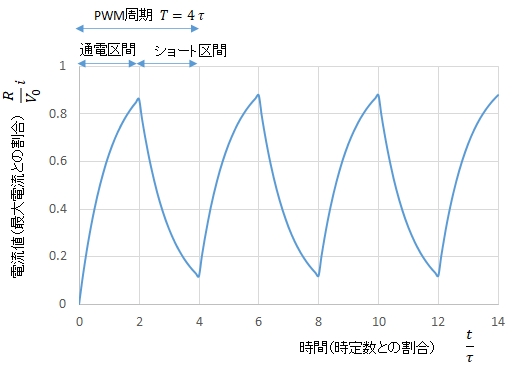
[定常解]
通電・絶縁駆動の1周期を通電区間・ショート区間を別々に考えます。
〇 通電区間の電流値初期値を \(i(0)=i_{ds}\) として,1周期経過後に再び電流値が \(i_{ds}\) になるとして
$$i_{ds}= \dfrac{V_0}{R} \dfrac{\exp(\dfrac{1}{\tau}Td)-1}{1-\exp(-\dfrac{1}{\tau}T)} \exp(-\dfrac{1}{\tau}T) \tag{17}$$
が得られます。
〇 ショート区間の電流初期値は
$$i_{ss} = \dfrac{V_0}{R} \dfrac{1-\exp(-\dfrac{1}{\tau}Td)}{1-\exp(-\dfrac{1}{\tau}T)} \tag{18}$$
で得られます。
そうすると,通電区間は,
$$i(t) = \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big)+i_{ds} \exp(-\dfrac{1}{\tau}t) \tag{19}$$
で表され,ショート区間は,ショート区間の開始を改めて \(t=0\) として
$$i(t) = i_{ss} \exp(-\dfrac{1}{\tau}t) \tag{20}$$
で表されます。
〇 例 \(P=4\) すなわちPWM周期 \(T = 4 \tau\) のとき,デューティ比 \(d=0.5\) では,電流値は次のグラフのようになります。
各周期では同じ電流波形が見られます。
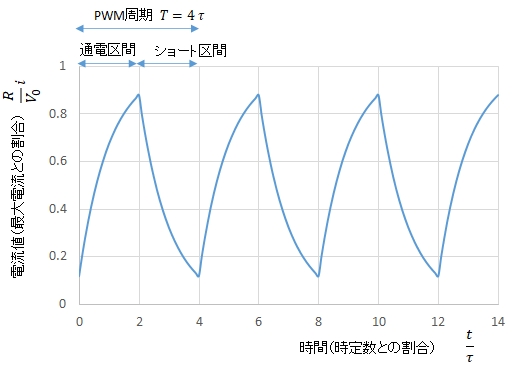
電流波形の最大値は \(i_{ss}\) で,最小値は \(i_{ds}\) になります。
5.2.2 電流の実測
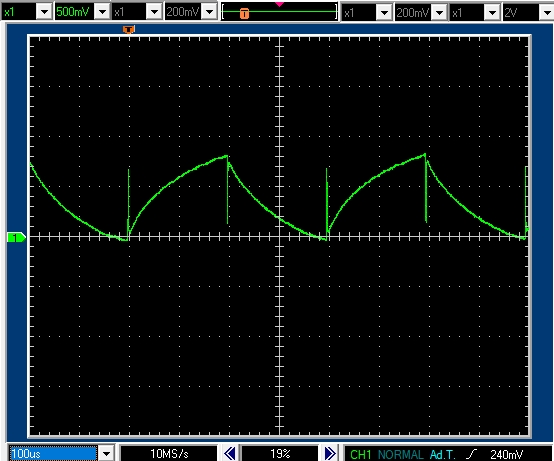
次の図は,\(P \risingdotseq 4\) すなわちPWM周期 \(T \risingdotseq 4\tau\) (実際にはPWM周期0.4msec)のとき,デューティ比 \(d=0.5\) のときの電流値を実際に測定したものです。
モータ軸は固定して,モータと直列に \(1\Omega\) の抵抗を挿入し,その両端電位差から測定しています。
\(T\)の測定精度はそれほど良くないので,計算値とのずれは仕方がないと考えられます。
5.2.3 平均電流値の計算
平均電流値 \(i_m\) は,1周期の電流を積分して1周期の長さで割ることで求められます。
1周期の間に,通電区間の立ち上がり,ショート区間の立ち下りがあるので,積分は通電区間( \(I_d\) )とショート区間( \(I_s\) )に分けて行います。
なお,時刻 \(0\) はそれぞれの区間開始に合わせています。
$$\begin{eqnarray}
I_d &=& \int ^ {Td}_0 \Big\{ \dfrac{V_0}{R} \Big(1-\exp(-\dfrac{1}{\tau}t)\Big)+i_{ds} \exp(-\dfrac{1}{\tau}t) \Big\} dt \tag{21}
\\
I_s &=& \int ^ {T (1-d)}_0 \Big\{ i_{ss} \exp(-\dfrac{1}{\tau}t) \Big\} dt \tag{22}
\end{eqnarray}$$
これを計算すると
$$\begin{eqnarray}
i_m &=& \dfrac{I_d+I_s}{T}
\\
&=& \dfrac{V_0}{R} \Big( T d - \tau \ \dfrac{\exp(-P)-\exp(Pd-P)-\exp(-Pd)+1}{1-\exp(-P)} \Big)
\\
&& - \dfrac{V_0}{R} \ \tau \ \dfrac{\exp(Pd-P)-1-\exp(-P)+\exp(-Pd)}{1-\exp(-P)}
\\
&=& \dfrac{V_0}{R}\ d
\tag{23}\end{eqnarray}$$
となって,平均電流値は \(d\) (デューティ比)で指示したとおりになることを示しています。(\(P= T / \tau\) に依存しません。)
グラフに表すと次のように単純です。
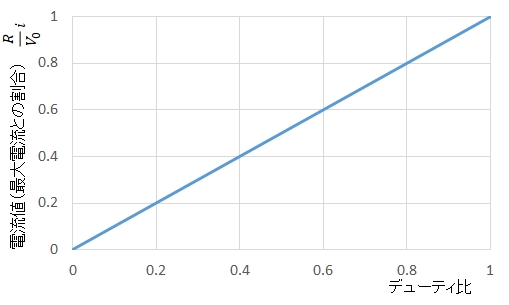
デューティ比と平均電流値は比例しており,これはデューティ比と発生トルクが比例していることを表しています。
6 まとめ
DCブラシモータのPWM駆動において停止から,低デューティ比で駆動を開始するとき,トルクが小くて,始動に苦労すると言われています。この真偽を検証しました。
DCブラシモータ駆動系をモデル化し,計算によって過渡解および定常解を求めることにしました。
DCブラシモータをモータドライバICを利用してPWM駆動を行う方式には,通電・絶縁駆動,通電・ショート駆動の2通りあります。
それぞれについて,低デューティ比駆動の場合,PWM周期と電流の関係を考えました。
PWM周期と平均電流を計算し,電流波形を計算と実測とで比較し,比較的よい一致が見られました。
PWM周期を短くすると,モータ駆動系の時定数に近づきますが,通電・ショート駆動方式では,デューティ比に比例した電流が流れるのに対し,通電・絶縁駆動方式では,デューティ比に比例した電流よりかなり少ない電流になってしまうのが確認できました。
DCブラシモータのPWM駆動において停止から,低デューティ比で駆動を開始するとき,トルクが小くて,始動に苦労するというのは,通電・絶縁駆動方式の時に起こる現象だということを確認しました。
通電・ショート駆動方式では,デューティ比に比例した電流になることが確認されました。
なお,ここでは触れなかったのですが,中高デューティ比の時には,通電・ショート駆動方式では,ショート区間でショートブレーキが作用してしまい,モータの回転が遅くなります。
2つの駆動方式のうち用途によって使い分けるのが良いと思います。