再帰を用いたプログラム

Copyright(C) 14Jan2007 coskx

関数が自分自身を関数として呼び出すことを「再帰」という。
プログラムのあるものは「再帰」を使わないと書けないばあいもある。またあるものは再帰を使ったほうが見通しよくプログラミングできる場合もある。


１．再帰の導入



次のプログラムは通常の関数を幾つか連続して呼び出しているプログラムである。func1()からfunc4（）はほぼ同じ内容である。
List 9.1.1 再帰導入のためのプログラム
class XXXX {
    public static void main(String args[]) {
        XXXX mainprg = new XXXX();
    }
 
    XXXX() {
        method1(3);
    }

    private void method4( int n) {
        System.out.printf("%d\n",n);
    }

    private void method3( int n) {
        System.out.printf("%d\n",n);
        if (0<n) method4(n-1);
    }

    private void method2( int n) {
        System.out.printf("%d\n",n);
        if (0<n) method3(n-1);
    }

    private void method1( int n) {
        System.out.printf("%d\n",n);
        if (0<n) method2(n-1);
    }
}

/*** 実行結果 ***
3
2
1
0
****************/

同様のプログラムを自分で自分を呼び出す関数で作ってみよう。
自分で自分を呼び出す関数のことを再帰関数と呼び，このような構造のプログラムを再帰プログラムと呼ぶ。

List 9.1.2 再帰を用いて書きなおしたプログラム
class XXXX {
    public static void main(String args[]) {
        XXXX mainprg = new XXXX();
    }
 
    XXXX() {
        recmethod(3);
    }

    private void recmethod( int n) {
        System.out.printf("%d\n",n);
        if (0<n) recmethod(n-1);
    }
}

/*** 実行結果 ***
3
2
1
0
****************/

特別の場合にそれ以上自分自身を呼び出さない仕掛けを持たないと無限呼び出しになってしまう。
0<nの場合のみ自分自身を呼び出すことになっており，nは必ず1だけ減って呼び出しているため，無限呼び出しにならないようになっている。


 ２．簡単な再帰の例（１からｎまでの和を求める）


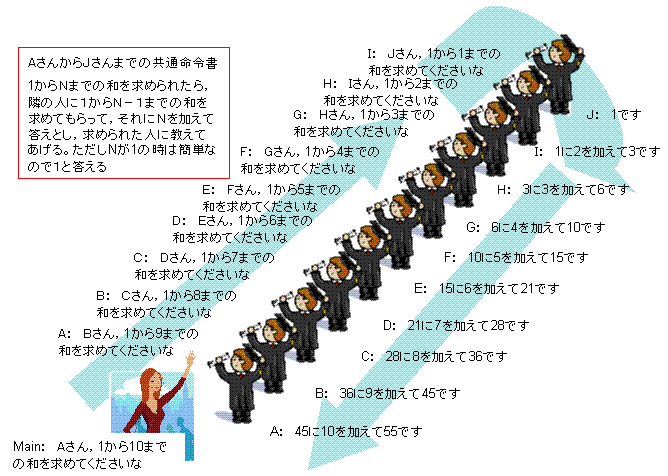
1から10までの和を求めるのに関数君に命令したら，実は関数君はめんどくさがり屋で，友人に下請け仕事に出して，自分は簡単な仕事だけで 済ませようとしていた。１からNまでの和を求めなさいといわれたら，1からN-1までの和を隣の人に計算してもらって，自分はその答えにNを加えて答えるというずうずうしさである。

それぞれの関数君は次のように考えていた。

A:「１から１０までの和」を求めるには，「１から９までの和」を求めたものに１０を加えればよい。
　　だからBさんに「１から９までの和」を求めてもらい，自分は１０を加えるだけ。
B:「１から９までの和」を求めるには，「１から８までの和」を求めたものに９を加えればよい。
　　だからCさんに「１から８までの和」を求めてもらい，自分は９を加えるだけ。
C:「１から８までの和」を求めるには，「１から７までの和」を求めたものに８を加えればよい。
　　だから・・・
　　　　　　　　　　　　　　　　　：
H:「１から３までの和」を求めるには，「１から２までの和」を求めたものに３を加えればよい。
　　だから・・・
I:「１から２までの和」を求めるには，「１から１までの和」を求めたものに２を加えればよい。
　　だから・・・
J:「１から１までの和」は１です。

それでも答えは55で正解であった。

実際のプログラムでは，10人の人間がいるわけではなく，自分の分身に作業をさせるようになっている。
ここで１からｎまでの和を求める関数を作りますが，自分自身を引数を変えながら呼び出すように作る。
また，１から1までの和を求める場合には１を返すように特別に設定する。
（特別の場合にそれ以上自分自身を呼び出さない仕掛けを持たないと無限呼び出しになってしまう。）
このように関数が自分自身を呼び出す形になるプログラムは再帰プログラムと 呼ばれる。

List 9.2.1 1から10までの和を求める

class XXXX {
    public static void main(String args[]) {
        XXXX mainprg = new XXXX();
    }
 
    XXXX() {
        int sum10;
        sum10=sumup(10);
        System.out.printf("sum up to %d : %d\n",10,sum10);
    }

    private int sumup( int n) {
        int ret;
        if (n==1) { /*無限呼び出しにならない保障*/
            ret= 1;
        } else {
            ret= sumup(n-1)+n;
        }
        return ret;
    }
}
実行結果
sum up to 10 : 55


再帰の関数を書くときには，どこかで無限呼び出しにならない保障を書いておかなければならない。
この例では，if (n==1) の時はそれ以上再帰呼び出しをしないようにしてある。


 

３．再帰の例（ハノイの塔）



こま数が４のハノイの塔

大きさの異なる４つのこまがあります。（右の図で#1〜#4）
こまを置くことができるのは3箇所（P0,P1,P2）です。
現在そのうちの1箇所（P0）に４つのこまが積んであります。
ゲームの目的は，積んであるこまを，すべて別の場所(ここではP2)に積みかえる事です。
ただし，積み替えの移動nioite
は一度のに１つのこましか動かせません。こまには大小関係があり，大きなこまの上に小さ
なこまを乗せるようにしか，こまを積むことができ
ません。移動の例はここにあります。PCに保存し
てから実行してください。

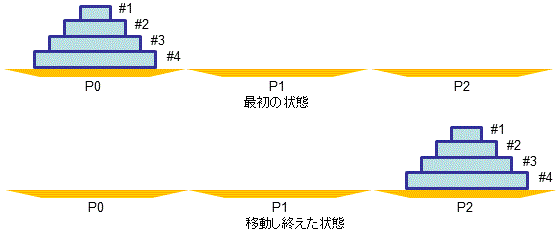以上のようなルールでP0からP2に塔を移動させる手順を見つけ出すことにする。
考え方は，次のようになります。
 #1〜#4をP0からP2に移すには，#1〜#3をP0からP1に移し，#4をP0からP2に移 し，#1〜#3をP1からP2に移せばよい。（「#1〜#3をP0からP1に移す」を別の関数に任せ，「#4をP0からP2に移す」を自分で行い，再び「#1〜#3をP1からP2に移す」を別の関数に任せる）
#1〜#3をP0からP1に移すには，#1〜#2をP0からP2に移し，#3をP0からP1に移し，#1〜#2をP2からP1に移せばよい。 （「#1〜#2をP0からP2に移す」を別の関数に任せ，「#3をP0からP1に移す」を自分で行い，再び「#1〜#2をP2からP1に移す」を別の関数に任せる）
　　　　　　　　　　　　　　　　　　：





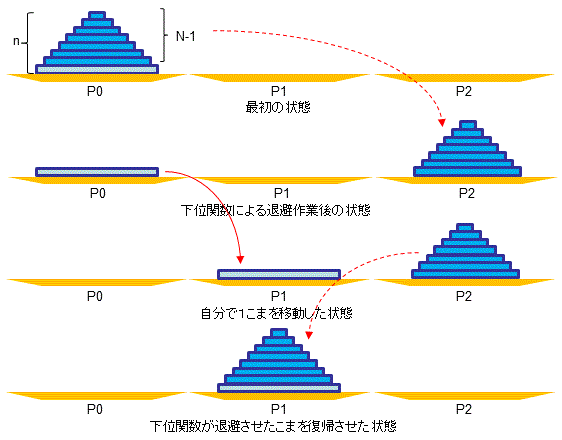
P0上のn個のこまを，P1に移動させるには
（１）別な関数に，P0上のn-1個のこまをP2に退避させるように頼み
（２）自分で，P0上の残りの大きいこまをP1に移動させ
（３）別な関数に，P2上に退避したn-1個のこまをP1に移動させるように頼む
という手順の関数を再帰呼び出しすればよい。

List 9.2.1 ハノイの塔

/* Hanoi.java */
class Hanoi {
    public static void main(String args[]) {
        Hanoi mainprg = new Hanoi();
    }
 
    Hanoi() {
        int number=NUMBER;
        int source=0;  /*移動元*/
        int destination=2; /*移動先*/
        movepile(number,source,destination);
    }

    private final int NUMBER = 4;
    private int count=0;

    private void movepile(int number,int source,int destination) {
        int temp;
        if (0<number) { /*無限呼び出しにならない保障(number==0ならなにもしない)*/
            /*tempは0,1,2のうちsourceでもdestinationでもない値になる*/
            temp=3-source-destination;

            /*sourceにあるnumber-1個のこまを場所tempに退避*/
            movepile(number-1,source,temp);

            System.out.printf("count=%4d : Move disk #%d from (P%d) to (P%d)\n",
                     ++count,number,source,destination);

            /*tempに退避していたnumber-1個のこまをdestinationへ*/
            movepile(number-1,temp,destination);
        }
    }
}
実行結果
count=   1 : Move disk #1 from (P0) to (P1)
count=   2 : Move disk #2 from (P0) to (P2)
count=   3 : Move disk #1 from (P1) to (P2)
count=   4 : Move disk #3 from (P0) to (P1)
count=   5 : Move disk #1 from (P2) to (P0)
count=   6 : Move disk #2 from (P2) to (P1)
count=   7 : Move disk #1 from (P0) to (P1)
count=   8 : Move disk #4 from (P0) to (P2)
count=   9 : Move disk #1 from (P1) to (P2)
count=  10 : Move disk #2 from (P1) to (P0)
count=  11 : Move disk #1 from (P2) to (P0)
count=  12 : Move disk #3 from (P1) to (P2)
count=  13 : Move disk #1 from (P0) to (P1)
count=  14 : Move disk #2 from (P0) to (P2)
count=  15 : Move disk #1 from (P1) to (P2)



 

４．バックトラック法を用いた騎士巡行 （ナイトツアー　Knight's tour）



チェス盤上をKnight（騎士）が動き回り，すべてのセルを訪問する経路を見つけるゲームである。
ただし，Knight（騎士）の動きは次の通りである。◇は現在位置を表し，○は移動可能なセルを表わす。

○ ○ ○ ○ ○ ○ ○
○ ○ ○ ○ ○ ○ ○
○ ○ ○ ○ ○ ○ ○
○ ○ ○ ◇ ○ ○ ○
○ ○ ○ ○ ○ ○ ○
○ ○ ○ ○ ○ ○ ○
○ ○ ○ ○ ○ ○ ○

チェス盤は８×８の大きさであるが，手始めに５×５の盤面について訪問順を見つけることにします。
左上を起点にして移動を開始する。全部の行き先を確かめてゆくが，ループだけでは探索を実現することが出来ない。
再帰を使って，あるセルに移動できたらその先を探す，そうでなかったら次の探索に移るというバックトラックの手法を使う。

盤の大きさの二次元配列を作り，盤をイメージする。未訪問のセルには０を，既訪問のセルには訪問順を表す自然数を格納してゆく。
盤の端のチェックを考えるとプログラムが大変になるので，周囲に２列余分に配列を作り，−１を埋めておく。
そして，あるセルが０だったらそのセルに動くことが可能であるを判断すればよいことになる。

-1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 １ 0 0 0 0 -1 -1
-1 -1 0 0 0 0 0 -1 -1
-1 -1 0 0 0 0 0 -1 -1
-1 -1 0 0 0 0 0 -1 -1
-1 -1 0 0 0 0 0 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1


ソースプログラム Knight5.c

/* Knight5.java */
/******************************************************
５×５の盤面でのチェスのknightの移動で盤面すべてのセルを
通過する手順を見つけて表示します。
５×５の配列をつくり，訪問していないところには０を埋め
訪問したところには，訪問順番号を書きます。
ただし盤面端のチェックを簡単にするため，周囲外側に２列
多く配列をつくり，?１を埋めておきます。
   x 0 1 2 3 4 5 6 7 8
 y                 
 0  -1-1-1-1-1-1-1-1-1
 1  -1-1-1-1-1-1-1-1-1
 2  -1-1 0 0 0 0 0-1-1
 3  -1-1 0 0 0 0 0-1-1
 4  -1-1 0 0 0 0 0-1-1
 5  -1-1 0 0 0 0 0-1-1
 6  -1-1 0 0 0 0 0-1-1
 7  -1-1-1-1-1-1-1-1-1
 8  -1-1-1-1-1-1-1-1-1
******************************************************/

class Move {
    int x;
    int y;
    Move(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

class Knight5 {
    public static void main(String[] args) {
        Knight5 mainprg = new Knight5();
    }

    Knight5() {
        int x,y;
        initBoard();
        counter=1;
        x=2;
        y=2;
        board[y][x]=counter;
        knighttour(x,y);
    }

    private int[][] board= new int[5+4][5+4]; //盤面配列
    private Move[] move= new Move[] {
        new Move(2,1),
        new Move(1,2),
        new Move(-1,2),
        new Move(-2,1),
        new Move(-2,-1),
        new Move(-1,-2),
        new Move(1,-2),
        new Move(2,-1)
    };                                        //一手の移動量の全種類
    private int counter;                      //手数カウンタ
    private int found=0;                      //見つけた巡回方法の個数

    private void printBoard() {//盤面の全表示
        int i,j;
        System.out.printf("Tour #%d is found.\n",++found);
        for (i=2; i<7; i++) {
            for (j=2; j<7; j++) {
                System.out.printf("%4d",board[i][j]);
            }
            System.out.printf("\n");
        }
        //if (found==3) exit(1); //３つ見つけたら終了
    }

    private void knighttour(int x, int y) {
    // 盤面の座標(x,y)にknightがいる状態から次の動作を試行する
        int i;
        int nextx, nexty;    //次の座標(nextx,nexty)
        for (i=0; i<8; i++) {
            nextx=x+move[i].x;
            nexty=y+move[i].y;
            if (board[nexty][nextx]==0) {
                //座標(nextx,nexty)は空だったので
                board[nexty][nextx]=++counter;
                if (counter==25) { /*無限呼び出しにならない保障*/
                    //最後まで埋まったので
                    printBoard();
                } else {
                    knighttour(nextx,nexty);
                }
                board[nexty][nextx]=0;
                --counter;
            }
        }
    }

    private void initBoard() { //盤面の初期化
        int i,j;
        for (i=0; i<9; i++) {
            for (j=0; j<9; j++) {
                board[i][j]=-1;
            }
        }
        for (i=2; i<7; i++) {
            for (j=2; j<7; j++) {
                board[i][j]=0;
            }
        }
    }
}
実行結果

Tour #1 is found.
   1  14  19   8  25
   6   9   2  13  18
  15  20   7  24   3
  10   5  22  17  12
  21  16  11   4  23
Tour #2 is found.
   1  12   7  16  25
   6  17   2  13   8
  11  20  15  24   3
  18   5  22   9  14
  21  10  19   4  23
Tour #3 is found.
   1  12   7  14  25
   6  15   2  19   8
  11  20  13  24   3
  16   5  22   9  18
  21  10  17   4  23

　　　　途中省略

Tour #303 is found.
   1   4   9  16  21
  10  15  20   3   8
   5   2  11  22  17
  14  19  24   7  12
  25   6  13  18  23
Tour #304 is found.
   1   4   9  18  21
  10  17  20   3   8
   5   2  13  22  19
  16  11  24   7  14
  25   6  15  12  23

実行結果を画面でなくファイルに保存する簡単な方法を与える。
GoAndSave.cmd　 をダウンロードして，作成されたファイルxxxx.javaをこの　GoAndSave.cmd　 の上にドラッグ＆ドロップする。
本来画面に表示される内容はテキストファイルxxxx_out.txtに書き込まれる。

 課題

 

（１）キーボードから整数ｎを受け取りｎ階乗を求めるプログラムを再帰を用いて作りなさい。 （p10ex01.java）
次の検証用mainを使いなさい。

int factorial(int n)
{
    この中身を自分で作る
}

メイン部
{
    int i;
    int fact;
    for (i=1; i<=12; i++) {
        fact=factorial(i);
        printf("factorial(%d)=%d\n",i,fact);
    }
}

（２）エイトクイン（Eight Queen）というゲームがある。８×８のチェス盤に８つのクインを置くゲームである。ただしクインはお互いに移動が自由でなければならない。すなわち自 分の移動可能領域に他のクインがいてはいけない。クインの移動可能領域とは，前後左右両斜め方向すべてのセルである。表示例にあるように，８つのクインの 置き方をすべて見つけなさい。表示例 （p10ex02.java）
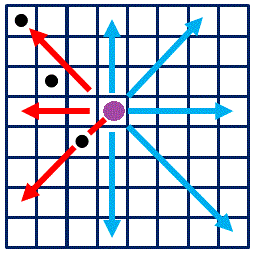
Queen（クイン）の動きは次のとおりである。◆はクインの現在位置(3,4)を表し，○は移動可能なセルを表わす。行(row)は横方向の並びであり，列(column)は縦方向の並びを表わす。



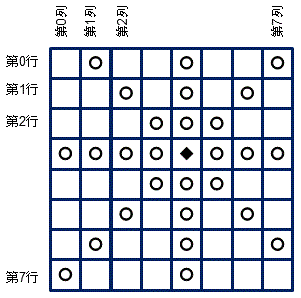
作業は第0列から順にクインを置くことにする。下図では●はすでに置かれたクインを表わしている。
現在(0,0)，(2,1)，(4,2)まで置いたところで，第3列に置こうとしているところである。
(3,3)に置けるかどうかをチェックしているところであるが，
水色の矢印方向はまだ何も置かれていないことは明らかなので
赤の矢印方向にすでに置かれたクインが存在するかどうかを確かめればよい。
図ではすでにクインが赤矢印上にあるので，(3,3)には新しいクインを置くことができない。



考え方

mainさん：0列目の作業をお願い

再帰関数Aさん：0列目をお願いされました。
「(0,0)に置けるかどうかチェックして置けるなら
(0,0)にQueenを置いてから
（0列目だから置けるのは当たり前）
再帰関数Bさんに1列目の作業をお願いする
(0,0)のQueenを取り去る」
同じ作業を、(1,0),(2,0)...(7,0)まで行う

再帰関数Bさん：1列目をお願いされました。
「(0,1)に置けるかどうかチェックして置けるなら
(0,1)にQueenを置いてから
再帰関数Cさんに2列目の作業をお願いする
(0,1)のQueenを取り去る」
同じ作業を、(1,1),(2,1)...(7,1)まで行う

再帰関数Cさん：2列目をお願いされました。
「(0,2)に置けるかどうかチェックして置けるなら
(0,2)にQueenを置いてから
再帰関数Dさんに3列目の作業をお願いする
(0,2)のQueenを取り去る」
同じ作業を、(1,2),(2,2)...(7,2)まで行う

再帰関数iさん：i列目をお願いされました。
「(0,i)に置けるかどうかチェックして置けるなら
(0,i)にQueenを置いてから
再帰関数i+1さんにi+1列目の作業をお願いする
(0,i)のQueenを取り去る」
同じ作業を、(1,i),(2,i)...(7,i)まで行う
骨組みの例

/*クインを置いてある場所は1，そうでない場所は0で表わすものとする。*/
public static void main(String[] args) {
    XXXX mainprg = new XXXX();
}
 
XXXX() {
    initBoard();
    columnwork(0);/*最初は第0列から作業を開始*/
}

private boolean[][] board= new boolean[8][8];

/* 他にも必要なメンバ変数があったらここに作る */

private void printBoard() {
    /* ８×８の盤面を表示 */
    /* 実装は自分で考えて */
}

/*column列に関する作業*/
private void columnwork(int column) {
    int row;
    int status;
    if (column==8) { /*column=8でこの関数が呼び出されたら，解が見つかっているということなので*/
        printBoard(); /*発見された解を表示*/
        return;
    }
    for (row=0; row<8; row++) {/*row=0～7まで検査*/

        /* ここでrow行column列の位置にクインがおけるかどうかのチェック */
        /* おけるならstatusには1,そうでなければ0が入っているようにする */
        /* 実装は自分 で                                                */
        if (status==1) { /*row行column列の位置にクインが置けるなら*/

            /* row行column列の位置にクインを置く */
            /* （board[8][8]のその位置を1にする）*/
            /* 実装は自分 で                      */

            columnwork(column+1); /*（column+1）列の作業をする*/

            /* row行column列の位置のクインをはずす */
            /* （board[8][8]のその位置を0にする）*/
            /* 実装は自分 で                        */
        }
    }
}

private void initBoard(void) {
    /* すべての盤面をクリア，初期状態にする */
    /* （board[8][8]のすべてを0にする）     */
    /* 実装は自分で考えて */
}

実行結果を画面でなくファイルに保存する簡単な方法を与えます。　GoAndSave.cmd　 をダウンロードして，作成されている実行形式ファイルxxxx.exeをこの　GoAndSave.cmd　 の上にドラッグ＆ドロップします。　本来画面に表示される内容はテキストファイルxxxx_out.txtに書き込まれます。

（３）騎士巡行につ いて８×８以上の場合（９×９，１０×１０，．．．）について最低3個の経路 を探しなさい。（発展課題）
探索時間が爆発的に増えるので，不要な探索は,はやめに発見し，打ち切るような改良が必要になる場合があります。
（p10ex03.java）

Pentium4（1.6GHz）ノートパソコンでの実行 例（実行結果，経過時間も表示されています，もっと早いプログラムを開発してください。）
５×５，６×６，7×７，．．．，３０×３０までの盤面で，それぞれ3つずつ解を探した例。　実行例　windows実行ファ イル例
６×６，８×８，．．．，３０×３０までの偶数×偶数のみで，しかも起点に戻る解をそれぞれ3つずつ探した例。　実行例　windows実行 ファイル例