グラフ

【１】関数のグラフ

Scilabはグラフ表示機能を持っています。関数のグラフを描いてみます。
グラフの描き方は大きく分けて2通りあります。

（１）独立変数数列-従属変数数列グラフ plot2d
独立変数を変化させた数列で行ベクトルをつくり，関数で従属変数数列を計算し，その数列で行ベクトルを作り，２つの行ベクトルを与えてグラフを描きます。

（２）独立変数数列-関数グラフ fplot2d
独立変数を変化させた数列で行ベクトルをつくり，関数で従属変数を計算しながらグラフを描きます。

【２】独立変数数列-従属変数数列グラフを描く場合の考え方 plot2d

2つの行ベクトルをつくり，その要素数を同一にします。例えば
P ：[ 2 4 6 8 ] ，Q ：[ 5 2 6 4 ]
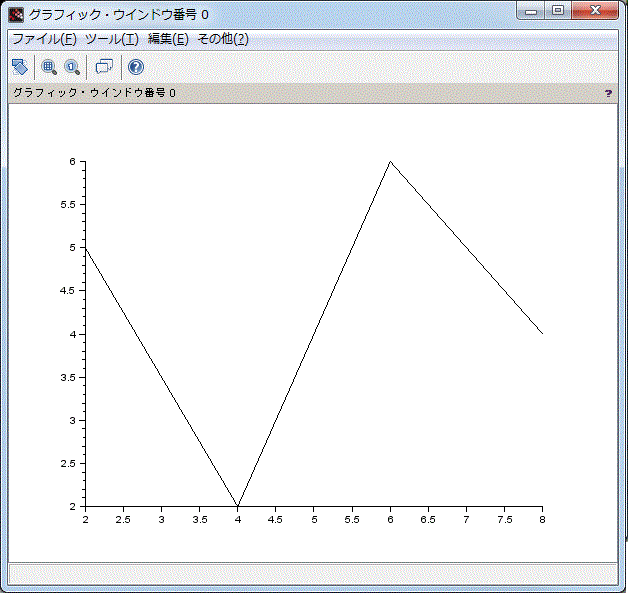
とすると，　(2,5),(4,2),(6,6),(8,4) の各座標点をプロットし，各点を結びます。
これがScilabにおけるグラフの基本的考え方です。

-->P=[2 4 6 8]
P =

2. 4. 6. 8.

-->Q=[5 2 6 4]
Q =

5. 2. 6. 4.

-->plot2d(P,Q)

Pの行ベクトルを作る

Qの行ベクトルを作る

P,Qの値を元にグラフを描く

P,Q点列によるグラフ

グラフが描けたら，画像をファイルに出力するか，Windowsのコピー＆ペーストを行うことができる。
（１）画像をファイルに出力：
　　　このウインドウのFileメニューからExportコマンドを選び，ダイアログで
　　　「Export」欄を「GIF」にするとGIFファイルが作成される。
（２）Windowsのコピー＆ペースト
　　　このウインドウのファイルメニューからクリックボードへコピーでEnhMetafileとして
　　　コピーし，MicrosoftWordなどで編集メニューから「形式を選択して貼り付
　　　け」コマンドで図（拡張メタファイル）で貼り付ける。

【３】独立変数数列-従属変数数列グラフ　（y = x² + 1 のグラフの例） plot2d

y = x² + 1 のグラフを描きます。
各コマンドの後ろに「;」をつけると，確認表示がなくなる。

-->clf();

-->x=[-3:0.1:3];

-->y=x^2+1;

-->plot2d(x,y);

グラフィックエリアのクリア

ｘを-3から3まで（増分0.1）の行ベクトルとする。

ｙをｘと同じサイズの行ベクトルとし，各要素をy=x^2+1で計算する。

行ベクトルｘとｙでプロットウインドウにプロットする。

y = x² + 1 のグラフ

【４】　スクリプトの利用

毎回，Scilabのウインドウに記述するのは面倒なので，テキストエディタで全スクリプトを書いておき，そこから実行する方法を行います。また「〜〜.sce」ファイルにスクリプトを保存しておき，ファイルを読み込ませて，すべてのスクリプトを実行手法を用います。

１）「Scilab」のコンソールウインドウの「アプリケーション」メニューを選ぶと，「SciNote」のウインドウが開くので，ここにスクリプトを記述します。

２）記述したスクリプトが次のようになったとします。（ここからコピー＆ペーストしてください）

clf();
x=[-3:0.1:3];
y=x^2+1;
plot2d(x,y);

３）「SciNote」のウインドウの「File」メニューの「保存」コマンドで，このスクリプトを適当なフォルダに保存してください。

４）「SciNote」の「実行」メニューの上の2つのうちのどちらかメニューを選ぶと，すべてのスクリプトを実行して，グラフを表示します。（「エコーバック付で・・・」だとコンソールに表示されます。）

スクリプトの利用は，グラフ描画だけでなく，一連の手続きを毎回行なうような場合に使用すると便利です。

【５】　グラフの詳細

（１）　グラフの軸オブジェクトの取得

もう一度 y = x² + 1 のグラフを描きます。これからの説明はスクリプトの利用を前提とします。
次のようなスクリプトを実行します。

clf();
x=[-3:0.1:3];
y=x^2+1;
plot2d(x,y);
a=get("current_axes"); //get the current axes
a.font_size=4;

グラフィックエリアのクリア
ｘを-3から3まで（増分0.1）の行ベクトルとする。
ｙをｘと同じサイズの行ベクトルとし，各要素をy=x^2+1で計算する。
行ベクトルｘとｙでプロットウインドウにプロットする。
グラフ表示カレント軸オブジェクトを取得　*1
そのオブジェクトのフォントサイズを変更　*2

*1　軸オブジェクトはグラフの軸に関する設定を持っているオブジェクトです。（実際にはもう少し広い範囲を表している）
　　軸オブジェクトが取得できたら，*2のようにその属性を設定できるようになる。（ここでは，軸目盛数字の大きさ）　　

y = x² + 1 のグラフ

（２）　軸オブジェクトの取得と詳細設定

再度y = x² + 1 のグラフを描きます。
Scilabオンラインhelpで「axes_properties」を検索するとよい。

clf();
x=[-3:0.1:3];
y=x^2+1;
plot2d(x,y,5,rect=[-3,0,3,10],nax=[3,7,1,6]);

a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid
a.labels_font_size=4;
a.title.text="y=x^2+1";
a.title.font_size=4;
a.x_label.text="x test";
a.x_label.font_size=4;
a.y_label.text="y test";
a.y_label.font_size=4;

xstring(-2,2,"myTestString1");
t=get("current_entity"); //get current_entity
t.font_style=2;
t.font_size=4;

xstring(-1.5,6,"myTestString2");
t=get("current_entity"); //get current_entity
t.font_style=3;
t.font_size=4;

グラフィックエリアのクリア
ｘを-3から3まで（増分0.1）の行ベクトルとする。
ｙをｘと同じサイズの行ベクトルとし，各要素はy=x^2+1となる。
行ベクトルｘとｙでプロットウインドウにプロットする。*1

カレント軸オブジェクトの取得
x,yの各グリッドを色番号2（青）で描く
軸目盛文字サイズの設定
タイトル"y=x^2+1"の表示
タイトルのフォントサイズの設定
x軸ラベル"x test"の表示
x軸ラベルのフォントサイズの設定
y軸ラベル"y test"の表示
y軸ラベルのフォントサイズの設定

文字列"myTestString1"を(-2,1)の位置に表示
カレントオブジェクト（ここでは文字列）を得る
文字列のフォントの設定
文字列のフォントサイズの設定

文字列"myTestString2"を(-1.5,6)の位置に表示
カレントオブジェクト（ここでは文字列）を得る
文字列のフォントの設定
文字列のフォントサイズの設定

*1　5は色番号であり，赤で描くことを示している。
　　rect=[-3,0,3,10]は，描画領域の左下が(-3,0)，右上が(3,10)であることを示している。
　　nax=[3,7,1,6]は，軸目盛の指示で，x軸副目盛個数=3，x軸主目盛個数=7，
　　y軸副目盛個数=1，y軸主目盛個数=6を示す。

y = x² + 1 のグラフ

plot2dのオプション
使用方法　plot2d(x,y,leg="f(x)=x^2+1",rect=[-3,0,3,10],nax=[4,6,2,5],style=[5,3]);

leg="f(x)=x^2+1"

凡例に表示する文字列（今後は使われない）

rect=[-3,0,3,10] 座標範囲の指定
rect=[xの左端，yの下端，xの右端，yの上端]

nax=[4,6,2,5] 座標メモリオプション
nax=[ｘの副目盛，xの主目盛，yの副目盛，yの主目盛]
この例ではxの副目盛4個，xの主目盛6個，
yの副目盛2個，yの主目盛5個

style=[5,3]
グラフのスタイルオプション
style=[グラフ色又は線種，凡例表示位置]
5は赤，3は左の上から3番目
色番号：1〜8，凡例表示位置：1〜6
凡例表示位置の自由度が低いため今後凡例位置表示は使われず，
legend関数に移行する。

frameflag=3
（例では未使用）
フレームオプション　値は0〜8
0：なにも計算しない　（デフォルト）
1：「rect」オプションに従う
2：x,yの最大最小から範囲自動計算
3：「rect」オプションに従い，ｘとｙは同じ目盛間隔
4：x,yの最大最小から範囲自動計算で，ｘとｙは同じ目盛間隔
5：「rect」オプションに従い，調整する
6：x,yの最大最小から範囲自動計算で，調整する
7：１と同じだが，以前のグラフは新目盛で再描画
8：２と同じだが，以前のグラフは新目盛で再描画

axesflag=4
（例では未使用）
軸オプション　値は0〜5
0：軸は描かない
1：y軸を左にして軸を描く
2：目盛なしで長方形で囲む
3：y軸を右にして軸を描く
4：ｘｙ軸を中央に配置して描く
5：ｘｙ軸が（0,0）に交差するように描く。（0,0）がない場合は軸を描かない

logflag="nn"
（例では未使用）

軸をリニア軸にするか対数軸にするかのオプション（Normal or Logarithmic）
ｘ：リニア，ｙ：リニア　　"nn"　（デフォルト）
ｘ：リニア，ｙ：対数　　　"nl"
ｘ：対数　，ｙ：リニア　　"ln"
ｘ：対数　，ｙ：対数　　　"ll"

xsetのオプション（今後使われない方向）

xset("wdim",500,300)

横500，縦300のグラフィックウインドウにする

xset("background",3) 背景の色設定

xset("font",2,4) フォント番号，フォントサイズの設定

xset("font size",3)
フォントサイズの設定

xset("use color",0)
白黒モード

xset("thickness",3)
グラフの線の太さの設定　1:1ピクセル

【６】　独立変数数列-従属変数数列グラフで，複数のグラフを同一面に描く plot2d

sin x ，sin 2x ，sin 3x を同一面に描く
複数グラフを描く場合は独立変数（横軸変数）を列ベクトルに取ります。
そしてグラフを描く従属変数の系列ごとに列ベクトルを作ります。

clf();
x=[-3:0.05:3]';

plot2d(x,[sin(x) sin(2*x) sin(3*x)],style=[1,2,3],..
nax=[3,7,1,7],rect=[-3,-1.5,3,1.5])

a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid
a.labels_font_size=4;
legend(["sinx","sin2x","sin3x"],1);

グラフィックエリアのクリア
ｘを-3から3まで（増分0.05）の列ベクトルとする。

プロットウインドウにプロットする。*1

カレント軸オブジェクトの取得
x,yの各グリッドを色番号2（青）で描く
軸目盛文字サイズの設定
凡例の表示 1は表示位置（右上）

*1 補足説明
１）コマンドが長すぎる時は「..」を打つと次の行につながる
２）style=[1,2,3]というのは色設定

sin x ，sin 2x ，sin 3x のグラフ

次のような記述もできる。

別な記述方法

clf();
x=[-3:0.05:3]';
y1=sin(x);
y2=sin(2*x);
y3=sin(3*x);
plot2d(x,[y1 y2 y3],style=[1,2,3],..nax=[3,7,1,7],rect=[-3,-1.5,3,1.5])
a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid
a.labels_font_size=4;
legend(["sinx","sin2x","sin3x"],1);

おまけ

SCILABはTexの表現もできるようになったので，もうすこし格好よくグラフが描ける。

sin x ，sin 2x ，sin 3x のグラフ（Texの表現を使って豊かに表現）

このグラフを描くスクリプトは次の通り。
ｘ軸は1/πした値で目盛を描く
ｘ軸目盛のπは後から文字列としてfor文で追加している。（表示位置の微調整が必要）

Texの表現を使って豊かに表現したグラフのスクリプト

clf();
x=[-1.1*%pi:0.05:1.1*%pi]';
xset("font size",3);
y1=sin(x);
y2=sin(2*x);
y3=sin(3*x);
xrad=x/%pi; //横軸のためにxを1/πにしたxradを作る
xtick=4;
plot2d(xrad,[y1 y2 y3],style=[[1,2,3],-1],..
nax=[4,xtick+1,0,7],rect=[-1,-1.5,1,1.5],axesflag=5);
xstring(0.4,1.0,"$\displaystyle y=\sin x$"); //Texの表現でy=sinxと表示
xstring(-0.9,1.0,"$\displaystyle y=\sin 2x$"); //Texの表現でy=sin2xと表示
xstring(0.4,-1.2,"$\displaystyle y=\sin 3x$"); //Texの表現でy=sin3xと表示
set(gca(),'data_bounds',[-1.1,1.1,-1.2,1.2]); //描画領域を変更
for n=0:xtick do
xstring(-0.94+n*0.5,-0.18,"$\displaystyle\pi$"); //横軸目盛にπを書き加える
end
a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid;

【７】　独立変数数列-関数グラフ fplot2d

あらかじめ関数を定義してからグラフを描きます。

例として　func(t) = exp ( - 0.1 t ) sin ( 2 t ) を定義して，　ｙ = func(t)　のグラフを描きます。
細かな表示設定は省略している。

clf();
deff('tmp=func(t)','tmp=exp(-0.1*t)*sin(2*t)')
t=[0:0.01:10];
fplot2d(t,func)

グラフィックエリアのクリア
関数の定義
ｔを0から10まで（増分0.01）の行ベクトルとする。
プロットウインドウにプロットする。

y = exp ( - 0.1 t ) sin ( 2 t ) のグラフ

plot2dのオプション使用方法　plot2d(x,y,leg="f(x)=x^2+1",rect=[-3,0,3,10],nax=[4,6,2,5],style=[5,3]);
leg="f(x)=x^2+1"	凡例に表示する文字列（今後は使われない）
rect=[-3,0,3,10]	座標範囲の指定 rect=[xの左端，yの下端，xの右端，yの上端]
nax=[4,6,2,5]	座標メモリオプション nax=[ｘの副目盛，xの主目盛，yの副目盛，yの主目盛] この例ではxの副目盛4個，xの主目盛6個， yの副目盛2個，yの主目盛5個
style=[5,3]	グラフのスタイルオプション style=[グラフ色又は線種，凡例表示位置] 5は赤，3は左の上から3番目色番号：1〜8，凡例表示位置：1〜6 凡例表示位置の自由度が低いため今後凡例位置表示は使われず， legend関数に移行する。
frameflag=3 （例では未使用）	フレームオプション　値は0〜8 0：なにも計算しない　（デフォルト） 1：「rect」オプションに従う 2：x,yの最大最小から範囲自動計算 3：「rect」オプションに従い，ｘとｙは同じ目盛間隔 4：x,yの最大最小から範囲自動計算で，ｘとｙは同じ目盛間隔 5：「rect」オプションに従い，調整する 6：x,yの最大最小から範囲自動計算で，調整する 7：１と同じだが，以前のグラフは新目盛で再描画 8：２と同じだが，以前のグラフは新目盛で再描画
axesflag=4 （例では未使用）	軸オプション　値は0〜5 0：軸は描かない 1：y軸を左にして軸を描く 2：目盛なしで長方形で囲む 3：y軸を右にして軸を描く 4：ｘｙ軸を中央に配置して描く 5：ｘｙ軸が（0,0）に交差するように描く。（0,0）がない場合は軸を描かない
logflag="nn" （例では未使用）	軸をリニア軸にするか対数軸にするかのオプション（Normal or Logarithmic）ｘ：リニア，ｙ：リニア　　"nn"　（デフォルト）ｘ：リニア，ｙ：対数　　　"nl" ｘ：対数　，ｙ：リニア　　"ln" ｘ：対数　，ｙ：対数　　　"ll"

xsetのオプション（今後使われない方向）
xset("wdim",500,300)	横500，縦300のグラフィックウインドウにする
xset("background",3)	背景の色設定
xset("font",2,4)	フォント番号，フォントサイズの設定
xset("font size",3)	フォントサイズの設定
xset("use color",0)	白黒モード
xset("thickness",3)	グラフの線の太さの設定　1:1ピクセル