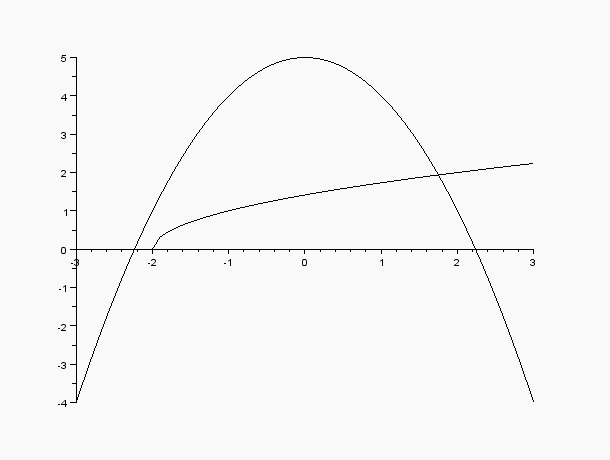いろいろな方程式

Copyright (C) 29Feb2004 coskx
last update Jan2012

【１】いろいろな方程式を解いてみよう

ここでは，連立方程式，高次方程式，無理方程式，超越方程式を解いてみます。

【２】連立方程式

連立方程式を係数行列A，未知数列ベクトルx，定数列ベクトルbを使って表すと
　A ｘ = b
の形で表されます。もし A が逆行列を持つなら
　A ^-1 A x = A ^-1 b ，　A ^-1 A = E 　（Eは単位行列）
なので
　x = A ^-1 b
で求められます。
 
例
 2 x₁ + 3 x₂ + 5 x₃ =  23
 3 x₁ - 5 x₂ -   x₃ = -10
-2 x₁ + 3 x₂ +   x₃ =   7

-->A=[ 2  3  5; -->    3 -5 -1; -->   -2  3  1]  A  =     2.    3.    5.      3.  - 5.  - 1.    - 2.    3.    1. -->b=[23 -10 7]'  b  =     23.    - 10.      7.  -->x=inv(A)*b  x  =     1.      2.      3.

係数行列Aを定義する。 定数列ベクトルbを定義する 「'」は転置を表す 逆行列演算で解列ベクトルを求める

解は

x₁ = 1
x₂ = 2
x₃ = 3

となり正解です。

【３】高次方程式

高次方程式を解きます。
（１）例１　x³ - 6 x² + 11 x - 6 = 0

-->x=poly(0,'x')  x  =     x -->p=x^3-6*x^2+11*x-6  p  =                 2   3   - 6 + 11x - 6x + x -->roots(p)  ans  =     3.      2.      1.

変数xを定義する。 （補足説明へ　→　） 多項式を定義する。（=0は書かない） 「roots」関数で「p=0」の解を求める。

x=1 or 2 or 3 が求められました。

（２）　例２　x⁴ + 2 x³ + 7 x² - 18 x + 26 = 0

-->x=poly(0,'x')  x  =     x -->q=x^4+2*x^3+7*x^2-18*x+26  q  =                  2    3   4     26 - 18x + 7x + 2x + x -->roots(q)  ans  =   - 2. + 3.i    - 2. - 3.i      1. + i        1. - i

変数xを定義する。 （補足説明へ　→　） 多項式を定義する。（=0は書かない） 「roots」関数で「q=0」の解を求める。 解の表現で「i」は虚数単位である。

x= 1+i, 1-i, -2+3i, -2-3i が求められました。

【４】無理方程式

次の無理方程式を解きます。
( x + 2 )^0.5 = - x² + 5

（１）第1段階　グラフを描いて，解の存在を確かめます。

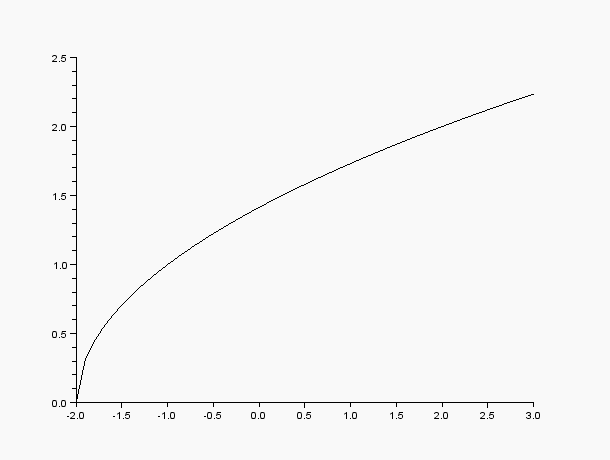
-->x1=[-2:0.1:3]; -->y1=sqrt(x1+2); -->plot2d(x1,y1);

xの定義域は-2≦xなので，この範囲でグラフを描く用意をします。 （xは行ベクトルになります。値の横方向羅列-2,-1.9,-1.8.-1.7,...,2.9,3） yの値を計算します。 （yも行ベクトルになります。値の横方向羅列。要素数はｘと同じ。）） x,yを表として値をプロットします。

y = ( x + 2 )0.5 のグラフ

-->x2=[-3:0.1:3]; -->y2=-x2^2+5; -->plot2d(x2,y2,frameflag=8);   -->a=get("current_axes"); //get the current axes   -->a.x_location="origin";

xを定義して，この範囲でグラフを描く用意をします。 （xは行ベクトルになります。値の横方向羅列-3,-2.9,-2.8.-3.7,...,2.9,3） yの値を計算します。 （yも行ベクトルになります。値の横方向羅列。要素数はｘと同じ。）） x,yを表として値をプロットします。 「frameflag=8」は直前のグラフを再描画して書き足すオプションです。 軸オブジェクトの取得 ｘ軸を原点通過で描く

y = ( x + 2 )0.5 と y = - x2 + 5 のグラフ

解は２つの曲線の交点すなわち，1.7の付近にあることがわかる。

（２）第2段階　解が1.7付近にあることを前提に，解を数値的に求めます。

{ ( x + 2 )^0.5 } - { - x² + 5 } = 0 を求めるために
関数 myfunc(x) = { ( x + 2 )^0.5 } - { - x² + 5 } を定義し,「fsolve」関数で解を見つけます。

-->deff('y=myfunc(x)','y=sqrt(x+2)+x^2-5'); -->fsolve(1.7,myfunc)  ans  =     1.7502683 -->[x_ans,v,info]=fsolve(1.7,myfunc)  info  =     1.  v  =     8.882E-16  x_ans  =     1.7502683

myfunc(x) = { ( x + 2 )0.5 } - { - x2 + 5 } を定義します。 （関数の定義の仕方　→ ） 「fsolve」関数で 1.7を探索の初期値として myfunc(x)=0 を数値的に解きます。 「fsolve」関数で評価しながらもう一度解きます。 info=1:解探索成功 v=8.882E-16(8.882×10-16)：解の精度 すなわちmyfunc(1.7502683の内部表現)の値

解　1.7502683　が見つかりました。

【５】超越方程式

tan x = 1/x ，（0.1<x<1.5）を解きます。
f(x) = tan x -1/x において f(x) = 0 を求めます。

（１）第1段階　グラフを描いて，解の存在を確かめます。

-->x=[0.1:0.01:1.5]'; -->one=ones(x); -->y1=tan(x); -->y2=one./x; -->y=y1-y2; -->plot2d(x,y);   -->a=get("current_axes"); //get the current axes   -->a.x_location="origin";   -->a.y_location="origin";

xを定義して，この範囲でグラフを描く用意をします。 （xは列ベクトルになります。値の縦方向羅列0.1,0.11,0.12,0.13,....,1.48.1.49,1.5） ｘと同じ要素数を持つ列ベクトルで要素の値がすべて1のものを作ります。 y1の値を計算します。 （y1も列ベクトルになります。値の縦方向羅列。要素数はｘと同じ。） y2の値を計算します。「./」演算は，要素ごとの割り算を意味します。 （y2も列ベクトルになります。値の縦方向羅列。要素数はｘと同じ。） yの値を計算します。「./」演算は，要素ごとの割り算を意味します。 （yも列ベクトルになります。値の縦方向羅列。要素数はｘと同じ。） x,yを表として値をプロットします。 軸オブジェクトの取得 ｘ軸を原点通過で描く ｙ軸を原点通過で描く

y = tan(x) + 1 / x のグラフ

解は0.85付近にあることがわかる。

fplot2dを用いた別なグラフの描き方（関数定義方法がわかればこちらのほうが簡単かも）

-->x=[0.1:0.01:1.5]';   -->deff('y=myfunc(x)','y=tan(x)-1/x');   -->fplot2d(x,myfunc);   -->a=get("current_axes"); //get the current axes   -->a.x_location="origin";   -->a.y_location="origin";

xを定義して，この範囲でグラフを描く用意をします。 （xは列ベクトルになります。値の縦方向羅列0.1,0.11,0.12,0.13,....,1.48.1.49,1.5） 関数を定義します。 xを独立変数として，関数で計算しながらプロットします。

（２）第2段階　解が0.85付近にあることを前提に，解を数値的に求めます。

関数 myfunc(x) = tan(x) - 1 / x  を定義し,「fsolve」関数で解を見つけます。

-->deff('y=myfunc(x)','y=tan(x)-1/x'); -->fsolve(0.85,myfunc)  ans  =      .8603336 -->[x_ans,v,info]=fsolve(0.85,myfunc)  info  =     1.  v  =     0.  x_ans  =      .8603336

myfunc(x) = tan(x) - 1 / x を定義します。 （関数の定義の仕方　→ ） 「fsolve」関数で 0.85を探索の初期値として myfunc(x)=0 を数値的に解きます。 「fsolve」関数で評価しながらもう一度解きます。 info=1:解探索成功 v=0：解の精度 すなわちmyfunc(.8603336の内部表現)の値

解　.8603336　が見つかりました。

補足

（１）多項式の定義と見かけ上の変数の定義

「poly」関数は多項式を定義します。定義の方法はいくつかあります。
（１）行ベクトル（要素数1の場合も含む）を与え，各要素を解とする有理方程式「多項式＝0」を与える多項式を作ります。
（２）係数を与え，多項式を作ります。
（３）行列を与え，固有値を求める方程式「多項式＝0」を与える多項式を作ります。

-->mypoly1=poly([2 3],'s')  mypoly1  =               2     6 - 5s + s	2と3を解とする有理方程式(s-2)(s-3)=0の左辺を作ります。 変数はsを使います。 (s-2)(s-3)を展開するとs^2-5s+6になります。
-->mypoly2=poly([2 -1],'x')  mypoly2  =              2   - 2 - x + x	2と-1を解とする有理方程式(x-2)(x+1)=0の左辺を作ります。 変数はxを使います。 (x-2)(x+1)を展開するとs^2-s-2になります。
-->mypoly3=poly([2 -1+%i -1-%i],'s')  mypoly3  =               3   - 4 - 2s + s	2と-1+iと-1+iを解とする有理方程式(s-2)(s+1-i)(s+1+i)=0 の左辺を作ります。 変数はsを使います。 (s-2)(s+1-i)(s+1+i)=を展開するとx^3-2s-4になります。
-->mypoly4=poly([2 -4 6],'s','coeff')  mypoly4  =                2     2 - 4s + 6s	係数を直接与えて多項式を作っています。
-->myMatrix=[2 4; 4 1]  myMatrix  =     2.    4.     4.    1. -->mypoly5=poly(myMatrix,'s')  mypoly5  =                2   - 14 - 3s + s	行列myMatrixを作ります。 myMatrixの固有値を計算する方程式は (2-s)(1-s)-4*4=0 左辺を展開すると s^2-3s-14 になります。
-->mypoly6=poly(12,'x')  mypoly6  =   - 12 + x	12を解とする有理方程式x-12=0の左辺を作ります。 変数はxを使います。
-->mypoly7=poly(0,'x')  mypoly7  =     x -->x=poly(0,'x')  x  =     x	0を解とする有理方程式x=0の左辺を作ります。 変数はxを使います。 0を解とする有理方程式x=0の左辺を作ります。 変数はxを使います。 左辺のxは式の名前，右辺のxは式を表しています。 この形は変数を定義したように見え，よく使用される定義である。
-->horner(mypoly5,2)  ans  =   - 16. -->horner(mypoly6,3)  ans  =   - 9. -->horner(mypoly7,4)  ans  =     4. -->horner(x,4)  ans  =     4.	「horner」関数を用いると， 各式の変数に値を代入した時の式の値を評価できる。 mypoly5(2) = -14-3*2+2^2 = -16 mypoly6(3) = -12+3 = -9 mypoly7(4) = 4 x(4) = 4

（２）ユーザ定義関数の定義
　（Scilabが最初から持っている関数以外で，ユーザが定義した関数をユーザ定義関数またはユーザ関数と呼ぶことにします。）

例として f(x) = sin ( 0.5 * x² ) を作ります。

ユーザ関数は次のように定義します。
deff(’仮の変数名(独立変数名) = ユーザ関数名’，’仮の変数名 = 独立変数を用いた関数の実体’)

（１）　単一のｘに対して計算すればよい場合

-->deff('myvar=myfunc(x)','myvar=sin(0.5*x*x)') -->myfunc(0.5)  ans  =      .1246747

ユーザ関数myfunc(x)を定義 yを計算する

（２）　xをベクトルとして扱う場合

-->x=poly(0,'x'); -->x=[0:0.01:6]; -->deff('myvar=myfunc(x)','myvar=sin(0.5*x.*x)') -->y=myfunc(x); -->plot2d(x,y);

変数xを定義 xの行ベクトルを定義 ユーザ関数myfunc(x)を定義 「x^2」は「x*x」ではなく「x.*x」（要素ごとの積） yを計算して行ベクトルにする グラフ表示

y =  sin ( 0.5 * x2 ) のグラフ