線型常微分方程式
Copyright (C) 29Feb2004 coskx
last
update Jan2012
【１】線型常微分方程式の入り口
定係数の線型常微分方程式をScilabで数値的に解きます。
ここでは
（１）定数係数一階線型非同次常微分方程式
（２）定数係数二階線型非同次常微分方程式の２つを取り上げます。
【２】定数係数一階線型非同次常微分方程式
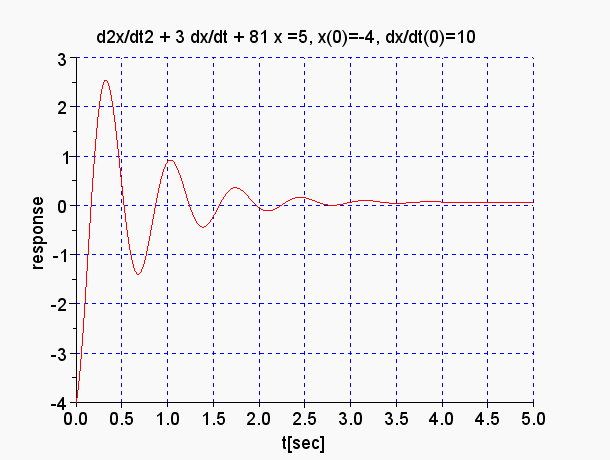
例 次の微分方程式を解きます。
d/dt x(t) + 3 x(t) = 5 （初期条件 x(0) = -4 ）
この微分方程式は解析的に解くことができ，
x(t) = 5/3 - 17/3 exp( -3 t )
である。 これを Scilab で数値的に解きます。与えられた微分方程式を
d/dt x(t) = - 3 x(t) + 5
と変形します。 Scilabの関数定義法に従って，次のように関数mydiffuncを作ります。
ODEとは ordinary differential equation のことである。ここではスクリプトを用いることにする。あるいは，スクリプトを全選択して，コピーし，Scilabのコンソールにペーストしてもよい。
clf();
deff("mydef=mydiffunc(t,x)","mydef=-3*x+5");
t0=0;x0=-4;t=[0:0.05:5]; //t: from 0 to 5 step 0.05
x=ode(x0, t0, t, mydiffunc);
plot2d(t,x,5);
a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid
a.labels_font_size=4; //目盛の数字
a.title.text="dx/dt+3x=5, x(0)=-4";
a.title.font_size=4;
a.x_label.text="t[sec]";
a.x_label.font_size=4;
a.y_label.text="response";
a.y_label.font_size=4;
Scilabの関数定義法に従って，関数mydiffuncを作る。
初期値，tの行ベクトルを作る。
「ode」関数でxの行ベクトル（長さはtと同じ）を作る。
赤でプロットする
カレント軸オブジェクトの取得
青グリッド
各タイトルの表示
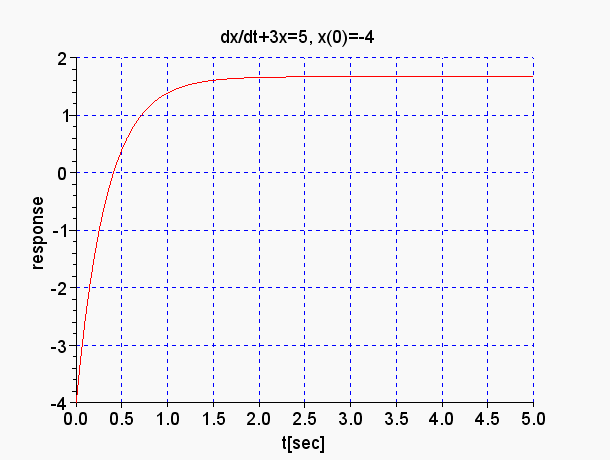
d/dt x(t) = - 3 x(t) + 5 の解グラフ
【３】定数係数二階線型非同次常微分方程式
例 次の微分方程式を解きます。
d2/dt2 x(t) + 3 d/dt x(t) + 81 x(t) = 5 （初期条件 x(0) = -4 ，d/dt x(0) = 10）
この微分方程式は解析的に解くことができ，減衰振動の形になることがわかっています。
これをSciLabで数値的に解きます。
ここで2階微分方程式を1階連立微分方程式に変形します。d/dt x(t) = v(t) とおくと次の連立微分方程式になります。
d/dt x(t) = v(t)
d/dt v(t) = -81 x(t) - 3 v(t) + 5これを行列表現にすると
| d/dt x(t) | | 0 1 | | x(t) | | 0 |
| | = | | | | + | |
| d/dt v(t) | | -81 -3 | | v(t) | | 5 |
（初期条件 x(0) = -4 ，v(0) = 10）となります。
clf();
deff("mydef=mydiffunc(t,x)","myMat=[0 1;-81 -3]; mydef=myMat*x+[0;5]");
t0=0;x0=[-4;10];t=[0:0.01:5]; //t: from 0 to 5 step 0.05
x=ode(x0, t0, t, mydiffunc);
plot2d(t,x(1,:),5)a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid
a.labels_font_size=4; //目盛の数字
a.title.text="d2x/dt2 + 3 dx/dt + 81 x =5, x(0)=-4, dx/dt(0)=10";
a.title.font_size=4;
a.x_label.text="t[sec]";
a.x_label.font_size=4;
a.y_label.text="response";
a.y_label.font_size=4;
Scilabの関数定義法に従って，関数mydiffuncを作る。
初期値，tの行ベクトルを作る。
「ode」関数でxの行列（2行で，行ベクトルの長さはtと同じ）を作る。
赤でプロットするグラフの詳細設定
d2/dt2 x(t) + 3 d/dt x(t) + 81 x(t) = 5 の解グラフ
（初期条件 x(0) = -4 ，d/dt x(0) = 10）なお，xは x(t) と d/dt x(t) の行列なので，xの転置の形で次のように内容を表示させることができます。
第1列が x(t) で第2列が d/dt x(t) です。
-->x'
ans =
- 4. 10.
- 3.8853423 12.90155
- 3.742598 15.614464
- 3.5737355 18.122685
- 3.3808731 20.412261
- 3.1662586 22.471394
- 2.9322458 24.290478
- 2.6812742 25.862099
- 2.4158463 27.181039
- 2.1385061 28.244248
- 1.8518171 29.050806
- 1.5583419 29.601866
- 1.2606212 29.900587
- 0.9611546 29.952041
- 0.6623818 29.763128
- 0.3666648 29.342457
- 0.0762714 28.700232
