一次遅れ要素,あるいは一次遅れ系は
T d/dt y(t) +
y(t) = kx(t)
( x(t):入力 y(t):出力 T,k:定数 )
で表されます。ラプラス変換により,伝達関数は
G(s) = k / ( Ts + 1 )
となります。ここで T=1,k=2 のもとで過渡応答を求めてみよう。
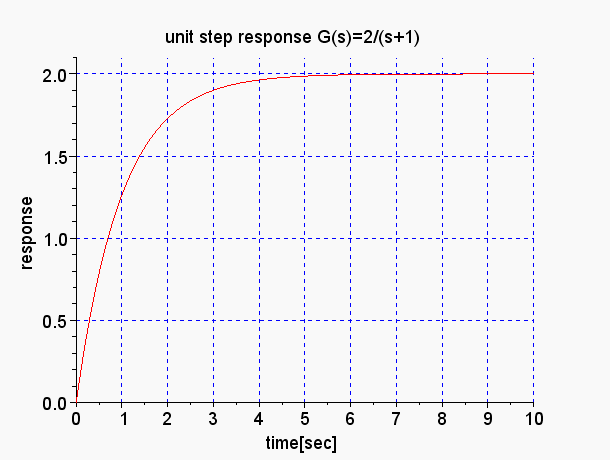
(1)単位ステップ応答
clf();
s=poly(0,'s');
G=2/(s+1);
mySys1=syslin('c',G);
t=[0:0.01:10];
y=csim('step',t,mySys1);
plot2d(t,y,5,rect=[0,0,10,2.1]);a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid
a.labels_font_size=4; //目盛の数字
a.title.text="unit step response G(s)=2/(s+1)";
a.title.font_size=4;
a.x_label.text="time[sec]";
a.x_label.font_size=4;
a.y_label.text="response";
a.y_label.font_size=4;
変数 s の定義(宣言としておこう)
伝達関数 G の定義
リニアシステム mySys1 の定義 「G」をもとに連続系('c')として定義
時間行ベクトル t の定義 [0 0.01 0.02 0.03 .... 9.98 9.99 10]
線形システム mySys1 のシミュレーション
ステップ入力とし,時刻データは時間行ベクトル t を用いる
シミュレーション結果は行ベクトル y に格納される赤でt-yグラフを描く。ただし値の範囲はt:0〜10,y:0〜2.1
グラフの詳細設定
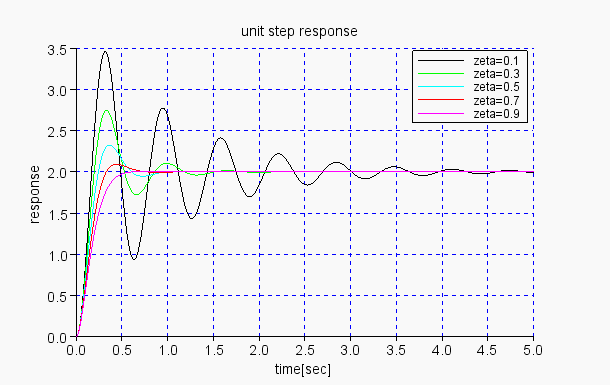
単位ステップ応答のグラフ
(2)周波数応答
リニアシステムの定義が済めば, bode 関数を用いてボード線図を描くことができます。
clf();
s=poly(0,'s');
G=2/(s+1);
mySys1=syslin('c',G);
bode(mySys1);f=get("current_figure");
f.children(1).grid=[2 2];
f.children(2).grid=[2 2];
f.children(1).labels_font_size=2; //目盛の数字
f.children(2).labels_font_size=2; //目盛の数字
f.children(1).x_label.font_size=2;
f.children(2).x_label.font_size=2;
f.children(1).y_label.font_size=2;
f.children(2).y_label.font_size=2;
変数 s の定義(宣言としておこう
伝達関数 G の定義
リニアシステム mySys1 の定義 「G」をもとに連続系('c')として定義
ボード線図を描く図の詳細設定
(オブジェクト"current_figure"のchildren(1)(2)は2つの図のAxes
をそれぞれ指している。)
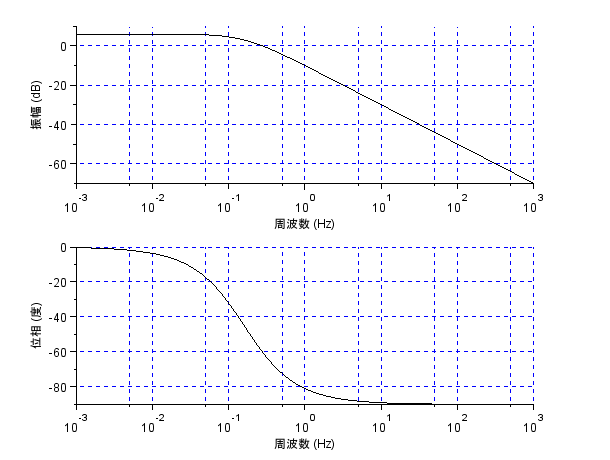
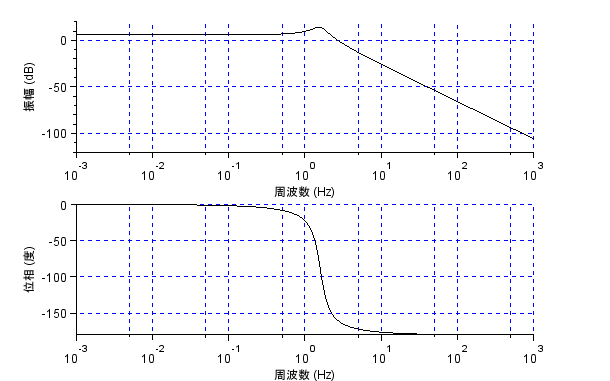
ボード線図 (周波数の単位はHz)
リニアシステムの定義が済めば, nyquist 関数を用いてナイキスト線図を描くことができます。
clf();
s=poly(0,'s');
G=2/(s+1);
mySys1=syslin('c',G);
nyquist(mySys1);a=get("current_axes"); //get the current axes
a.grid=[2 2]; //make x,y-grid
a.labels_font_size=2; //目盛の数字
a.title.font_size=2;
//a.x_location="origin";
//a.y_location="origin";
a.x_label.font_size=2;
a.y_label.font_size=2;
変数 s の定義(宣言としておこう)
伝達関数 G の定義
リニアシステム mySys1 の定義 「G」をもとに連続系('c')として定義
ナイキスト線図を描く図の詳細設定
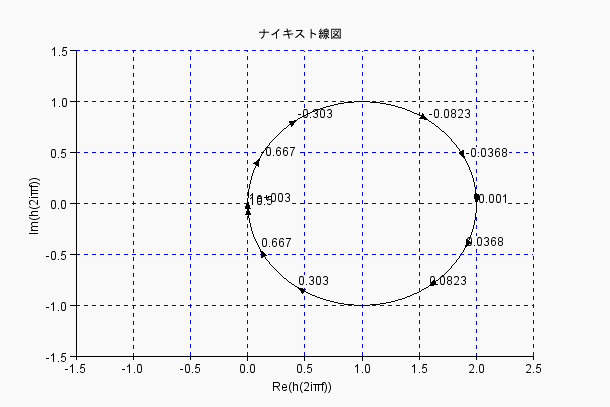
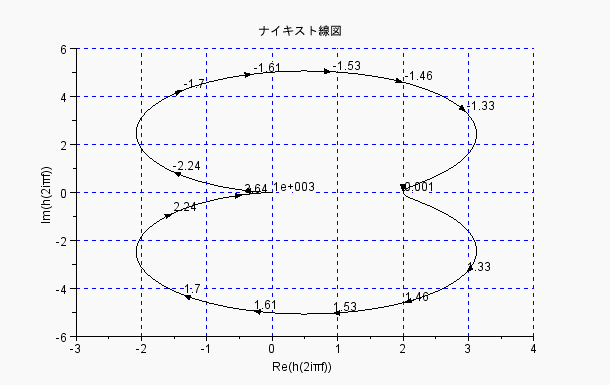
ナイキスト線図 (周波数の単位はHz)
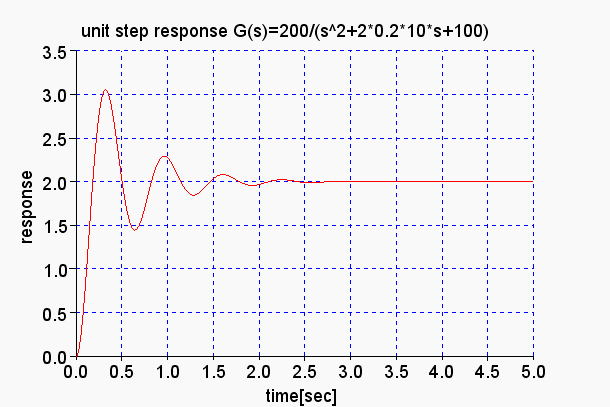
(3)状態空間のアプローチ
先に与えた一次遅れ要素の微分方程式の記述は
d/dt y(t) = -1/T y(t) + k/T x(t)
で表すこともできます。
状態空間表現ではA,b,cはそれぞれ1行1列の特別な場合の行列となります。
A=-1/T, b=k/T, c=1
次の記述でもリニアシステムの記述が可能です。
-->A=[-1]
-->b=[2];
-->c=[1];
-->mySys1=syslin('c',A,b,c);
補足 一般的な状態空間表現の扱いとsyslin関数
sl=syslin(dom,A,B,C [,D [,x0] ])
represents the system :
s x = A*x + B*u
y = C*x + D*u
x(0) = x0