制御工学への応用その２

【１】制御工学への応用

この文書はScilabの制御工学への応用を紹介をしています。

【２】ブロック線図から伝達関数を導く

ブロック線図が与えられた時，伝達関数を計算することができます。

例えば

     1
K= ------
    s+2
         200
G= ---------------
    s² + 4s + 100

とする時

（１）２つの要素の直列結合は K*G で表されます。（通常の表現）
            -----       -----
    ------>| K |---->| G |---->
            -----       -----

（２）２つの要素の並列結合は K+G で表されます。（通常の表現）
               -----
         ---->| G |----
        |      -----     |+
    ----|                o---->
        |      -----     |+
         ---->| K |----
               -----

（３）２つの要素のネガティブフィードバック結合は　G / (1+G K) で表される。（通常の表現）
あるいはScilab特有の表現として G/.K でもよい。
      +        -----
  -----o----->| G |----*----->
     - |      -----     |
       |       -----     |
        ------| K |←--
               -----

-->s=poly(0,'s');

-->G=200/(s^2+2*0.2*10*s+100)
G =

        200
    -----------
                2
    100 + 4s + s

-->K=1/(s+2)
K =

      1
    -----
    2 + s

-->K*G
ans =

            200
    -------------------
                   2   3
    200 + 108s + 6s + s

-->K+G
ans =

                    2
      500 + 204s + s
    ------------------
                   2   3
    200 + 108s + 6s + s

-->G/(1+G*K)
ans =

        400 + 200s
    ------------------
                   2   3
    400 + 108s + 6s + s

-->G/.K
ans =

        400 + 200s
    ------------------
                   2   3
    400 + 108s + 6s + s

変数 s の定義（宣言としておこう）

伝達関数 G の定義

伝達関数 K の定義

直列結合

並列結合

ネガティブフィードバック結合（表現１）

ネガティブフィードバック結合（表現２）

【３】安定な制御系と不安定な制御系

二次遅れ要素に一次遅れ要素が直列に結合した，直結フィードバックを考えます。

（１）　例１　安定な制御系

      1.5
K1 = ------
      s+2
         200
G= ---------------
    s² + 4s + 100

とする時

      +        ------       -----
  -----o----->|  K1 |---->| G |----*----->
     - |      ------       -----     |
        --------------←--------------

この系の単位ステップ応答を求めます。

-->s=poly(0,'s');

-->G=200/(s^2+2*0.2*10*s+100)
G =

        200
    -----------
                2
    100 + 4s + s

-->K1=1.5/(s+2)
K1 =

     1.5
    -----
    2 + s

-->TrFunc1=K1*G/.(1)
TrFunc1 =

            300
    -------------------
                   2   3
    500 + 108s + 6s + s

-->mySys1=syslin('c',TrFunc1);

-->t=[0:0.01:10];

-->y=csim('step',t,mySys1);

-->plot2d(t,y)

変数 s の定義（宣言としておこう）

伝達関数 G の定義

伝達関数 K1 の定義

ネガティブフィードバック結合の等価伝達関数

TrFunc1=K1*G/(1+K1*G) と同じ意味

リニアシステムmySys1に変換

時間行ベクトル t の定義

ステップ応答を求める

グラフ表示

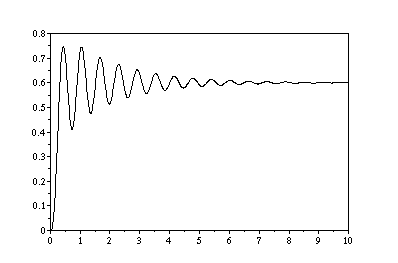
単位ステップ応答のグラフ
この応答は収束しているので制御系は安定である

（２）　例２　不安定な制御系

K1の分子を 1.5→2.5 と変更してK2に変更します。（Gは変更無し）

      2.5
K2 = ------
      s+2
         200
G= ---------------
    s² + 4s + 100

とする時

      +        ------       -----
  -----o----->|  K2 |---->| G |----*----->
     - |      ------       -----     |
        --------------←--------------

この系のインパルス応答を求めます。

-->s=poly(0,'s');

-->G=200/(s^2+2*0.2*10*s+100)
G =

        200
    -----------
                2
    100 + 4s + s

-->K2=2.5/(s+2)
K2 =

      2.5
    -------
     2 + s

-->TrFunc2=K2*G/.(1)
TrFunc2 =

            500
    -------------------
                   2   3
    700 + 108s + 6s + s

-->mySys2=syslin('c',TrFunc2);

-->t=[0:0.01:10];

-->y=csim('step',t,mySys2);

-->plot2d(t,y)

変数 s の定義（宣言としておこう）

伝達関数 G の定義

伝達関数 K2 の定義

ネガティブフィードバック結合の等価伝達関数

TrFunc2=K2*G/(1+K2*G) と同じ意味

リニアシステムmySys1に変換

時間行ベクトル t の定義

ステップ応答を求める

グラフ表示

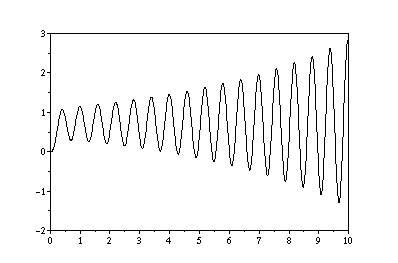
単位ステップ応答のグラフ
この応答は発散しているので制御系は不安定である

（３）安定判別

ここで取り上げた２例について，安定判別を行ないます。

（３．１）制御系の特性方程式の根による判別

制御系の特性方程式の根の実部が負であればその制御系は安定です。
すなわち「等価伝達関数（TrFunc1またはTrFunc2）の分母」＝0の方程式の根を求めてみます。

-->roots(denom(TrFunc1))
ans =

  - 0.5615219 + 10.10978i
  - 0.5615219 - 10.10978i
  - 4.8769561

-->roots(denom(TrFunc2))
ans =

    0.1752851 + 10.497409i
    0.1752851 - 10.497409i
  - 6.3505703

TrFunc1の特性方程式の根

根の実部が負なので「安定」

TrFunc2の特性方程式の根

根の実部が正なので「不安定」
(ステップ応答時の発振周波数はω=10.5rad/secなので1.67Hz)

（３．２）Routhの安定判別

特性方程式の係数からRouth数列の第１列がすべて同符号であれば制御系は安定です。

-->routh_t(denom(TrFunc1))
ans =

    1.           108.
    6.           500.
    24.666667    0.
    500.         0.

-->routh_t(denom(TrFunc2))
ans =

    1.           108.
    6.           700.
- 8.6666667    0.
    700.         0.

TrFunc1の特性方程式でRouth数列を作る

Routh数列の第１列がすべて同符号なので「安定」

　　特性方程式はs^3+6s^2+108s+500=0であった

TrFunc2の特性方程式でRouth数列を作る

Routh数列の第１列に異符号を含むので「不安定」

　　特性方程式はs^3+6s^2+108s+700=0であった

（３．３）　Nyquistの安定判別

一巡伝達関数（G*K1およびG*K2）のナイキスト線図を描き，周波数0から無限大にたどる時，-1を右に含まなければ，その制御系は安定です。

-->gk1=syslin('c',G*K1);

-->gk2=syslin('c',G*K2);

-->nyquist(gk1);

-->nyquist(gk2);

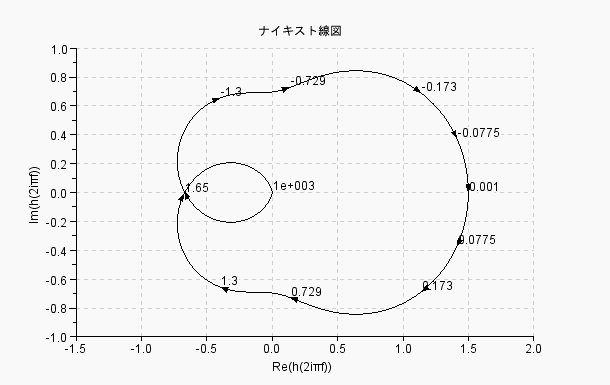
G*K1のナイキスト線図を描きます

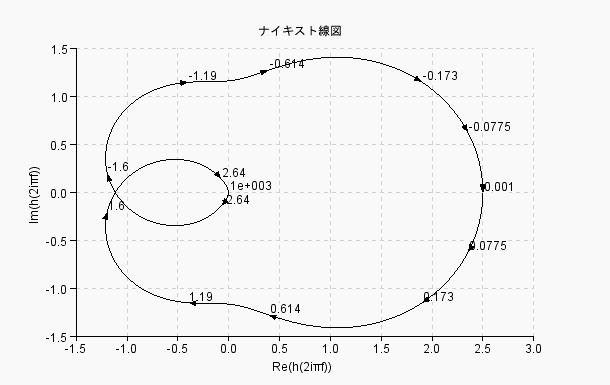
G*K2のナイキスト線図を描きます

ナイキスト線図　（周波数の単位はHz）
「-1+j0」を右側に見ないので安定

ナイキスト線図　（周波数の単位はHz）
「-1+j0」を右側に見るので不安定

（３．４）　位相余裕とゲイン余裕

一巡伝達関数（G*K1およびG*K2）を用いて，位相余裕（ゲインが1の時の位相余裕）とゲイン余裕（位相が-180°の時のdBゲインの余裕）

-->[phase1,freq1]=p_margin(gk1)
freq1 =

    0.3929061
phase1 =

    123.00942

-->[phase2,freq2]=p_margin(gk2)
freq2 =

    1.7108887
phase2 =

- 9.3527936

-->[gain1,freq11]=g_margin(gk1)
freq11 =

    1.6539867
gain1 =

    3.4831352

-->[gain2,freq21]=g_margin(gk2)
freq21 =

    1.6539867
gain2 =

- 0.9538398

G*K1の位相余裕（ゲインが１の時の位相余裕とその時の周波数[Hz]）

0.39Hz　のときゲイン＝1

位相余裕は123°（安定）

G*K2の位相余裕を求める

1.71Hz のときゲイン＝1

位相余裕は-9.4°（不安定）

G*K1のゲイン余裕（位相が-180°の時のdBゲイン）

1.65Hz　のとき位相＝-180°

ゲイン余裕は3.5dB（安定）

G*K2のゲイン余裕を求める

1.65Hz　のとき位相＝-180°

ゲイン余裕は-0.95dB（不安定）