　この概説は高速フーリエ変換FFTのアウトラインを解説する。高速フーリエ変換の解説書はそのアルゴリズムを記述したものがあるが，この概説は高速フーリエ変換アルゴリズム詳細は他に譲り，計算式は省き，高速フーリエ変換関数（内容には触れない）を用いて高速フーリエ変換によりデータがどのように変換されるかのみを述べる。具体的イメージを確立するために，マイクロフォンで捕らえ，ADコンバータで一定間隔でサンプリングされた音響データが「高速フーリエ変換」される場合を想定することにする。
　ここで議論する際，高速フーリエ変換のプログラムはC言語で書かれた小坂研究室で使用している表１．１の3つのファイルを用いることとする。読者は，マルチソースファイルでのプログラミングおよびコンパイルについて，またC言語の関数，関数の引数，複素数型をつくるための構造体についての知識があるものとする。

表１．１　使用するファイル
ファイル名	内容
common.h	複素数型の定義，Πの定義
fftcore.h	fftcore.hのプロトタイプ宣言
fftcore.c	高速フーリエ変換に関連する関数ライブラリ

　例えばDTMF（プッシュホンのピッポッパの音：Dual Tone Multi Frequency）音の例として，ボタン「０」および「1」を押したときの音を1024点サンプリングした波形を図２．１，２．３に示すが，これを見ただけでは，この音の性質はわからない。しかし図２．２，２．４のように高速フーリエ変換した「パワースペクトル」（詳細は８．パワースペクトルの計算）であらわすと，プッシュホンの１つのダイアルボタンを押した時の音は２つの周波数の音でできていることが分かり，どのボタンを押したときの音なのか知ることができる。

DTMFTIMEDOMAIN.GIF - 6,475BYTES

１ブロック＝1024サンプルを表示
サンプリング周波数は11025Hz
図２．３　DTMFの音の波形（ボタン「１」を押した時の音）

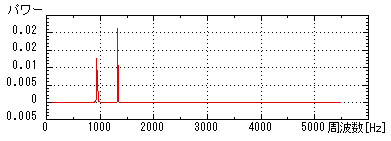
DTMFPOWERSPECTRUM.GIF - 2,864BYTES

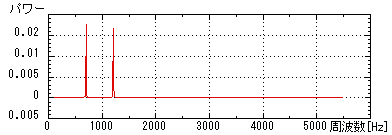
横軸は周波数，縦軸は音のパワー
697Hzと1209Hzの音の合成であることがわかる
図２．４　プシュボタン「１］に対応するDTMFの波形のパワースペクトル

　ADコンバータで一定間隔でサンプリングされた音響データは，音の波形を表し，「時間領域データ」の１種である。本来「時間領域データ」は無限に続くデータ列であるが，高速フーリエ変換では「時間領域データ」は512個，1024個など２のべき乗個のサンプルブロックで扱われる。そして，変換後は同じサンプル個数の「周波数領域データ（スペクトル；spectrum）」になる。「周波数領域データ（スペクトル；spectrum）」とは，変換前の「時間領域データ」にどのような周波数の音が，どのくらいの大きさで入っていたかを表す概念である。
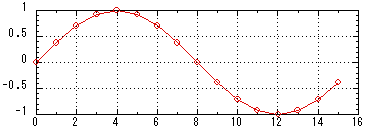
　実際のプログラムでは，「時間領域データ」は実数型変数の配列に格納されるが，「周波数領域データ（スペクトル；spectrum）」は複素数型配列に格納される。具体的なデータで高速フーリエ変換を行なってみよう。ここではデータブロック長は16とする。リスト３．１は１６サンプルで構成された正弦波の高速フーリエ変換を行なうプログラムである。関数maketimedomain()は「１６サンプルで構成された振幅１の1周期の正弦波」を作る関数である。表１．１にあげた3つのファイルとともにコンパイルと実行ができる。このプログラムを実行すると「１６サンプルで構成された振幅１の1周期の正弦波」はファイル「timedomain.txt」として保存され，グラフにすると図３．１のようになる。プログラムの途中で実数の「時間領域データ」は，虚部が0.0の複素数の「時間領域データ」となり「comptimedomain.txt」として保存される。高速フーリエ変換後のデータはファイル「spectrum.txt」として保存され，グラフにすると図３．２のようになる。

リスト３．１　１６サンプルで構成された正弦波の高速フーリエ変換

#include <stdio.h>
#include <math.h>
#include "common.h"
#include "fftcore.h"
#define SIZE 16

void maketimedomain(double x[],int size)
{
    int i;
    for (i=0;i<size;i++) {
        x[i]=sin((2*M_PI)*i/size);
    }
}

main()
{
    double timedomain[SIZE]; /*時間領域データ格納域*/
    dcomplex_t fftwork[SIZE]; /*複素数作業領域*/

    /*FFTの初期化*/
    initfft(SIZE);

    /*時間領域データの作成とファイル保存*/
    maketimedomain(timedomain,SIZE);
    savereal(timedomain,SIZE,"timedomain.txt");

    /*FFT作業の準備のため，時間領域データを複素数作業領域へ*/
    /*コピーとファイル保存*/
    real2cmp(timedomain,fftwork,SIZE);
    savecmp(fftwork,SIZE,"comptimedomain.txt");

    /*FFT（順方向フーリエ変換）*/
    /*作業領域fftworkの内容がスペクトルになる*/
    /*得られたスペクトルのファイルへの保存*/
    fft(1,fftwork,SIZE);
    savecmp(fftwork,SIZE,"spectrum.txt");

}

/**************     実行結果のはじまり    *************
ファイル「timedomain.txt」（時間領域データ）
   0    0.000000e+000
   1    3.826834e-001
   2    7.071068e-001
   3    9.238795e-001
   4    1.000000e+000
   5    9.238795e-001
   6    7.071068e-001
   7    3.826834e-001
   8    3.231085e-015
   9    -3.826834e-001
10    -7.071068e-001
11    -9.238795e-001
12    -1.000000e+000
13    -9.238795e-001
14    -7.071068e-001
15    -3.826834e-001

ファイル「comptimedomain.txt」（複素数化された時間領域データ）
（データは実部と虚部から成り立っているが，虚部は0.0である）
   0    0.000000e+000    0.000000e+000
   1    3.826834e-001    0.000000e+000
   2    7.071068e-001    0.000000e+000
   3    9.238795e-001    0.000000e+000
   4    1.000000e+000    0.000000e+000
   5    9.238795e-001    0.000000e+000
   6    7.071068e-001    0.000000e+000
   7    3.826834e-001    0.000000e+000
   8    3.231085e-015    0.000000e+000
   9    -3.826834e-001    0.000000e+000
10    -7.071068e-001    0.000000e+000
11    -9.238795e-001    0.000000e+000
12    -1.000000e+000    0.000000e+000
13    -9.238795e-001    0.000000e+000
14    -7.071068e-001    0.000000e+000
15    -3.826834e-001    0.000000e+000

ファイル「spectrum.txt」（複素数スペクトル）
（データは実部と虚部から成り立っている）
   0    1.984734e-016    0.000000e+000
   1    -6.175616e-016    -5.000000e-001
   2    2.093026e-016    -6.618772e-016
   3    3.878632e-016    -3.469447e-016
   4    2.019428e-016    -2.324529e-016
   5    2.220446e-016    -1.318390e-016
   6    1.945830e-016    -7.901015e-017
   7    7.764412e-016    0.000000e+000
   8    2.054123e-016    0.000000e+000
   9    1.734723e-016    1.110223e-016
10    1.945830e-016    7.901015e-017
11    4.156187e-016    3.469447e-016
12    2.019428e-016    2.324529e-016
13    2.220446e-016    4.649059e-016
14    2.093026e-016    6.618772e-016
15    -3.195466e-015    5.000000e-001

***************     実行結果のおわり    **************/

（データ番号16で0にもどるはず）
ファイル「timedomain.txt」
図３．１　１６サンプルで構成された正弦波の時間領域波形

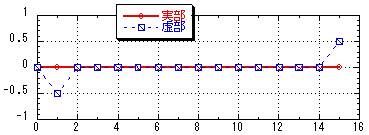
ファイル「spectrum.txt」
図３．２　１６サンプルで構成された正弦波のスペクトル

リスト３．１の関数maketimedomain()をリスト４．１のように変更すると図４．１の時間領域データと図４．２のスペクトルができる。時間領域波形は，「１６サンプルで構成された振幅２の3周期の正弦波」である。

リスト４．１　maketimedomain()の変更

void maketimedomain(double x[],int size)
{
    int i;
    for (i=0;i<size;i++) {
        x[i]=2.0*sin(3.0*(2*M_PI)*i/size);
    }
}

/**************     実行結果のはじまり    *************
ファイル「timedomain.txt」（時間領域データ）
    0    0.000000e+000
   1    1.847759e+000
   2    1.414214e+000
   3    -7.653669e-001
   4    -2.000000e+000
   5    -7.653669e-001
   6    1.414214e+000
   7    1.847759e+000
   8    1.849833e-014
   9    -1.847759e+000
10    -1.414214e+000
11    7.653669e-001
12    2.000000e+000
13    7.653669e-001
14    -1.414214e+000
15    -1.847759e+000

ファイル「spectrum.txt」（複素数スペクトル）
（データは実部と虚部から成り立っている）
   0    1.225535e-015    0.000000e+000
   1    1.229404e-015    2.775558e-016
   2    1.126707e-015    2.744484e-015
   3    -5.372134e-015    -1.000000e+000
   4    1.045123e-015    -2.983724e-015
   5    1.870642e-015    -1.110223e-015
   6    1.185585e-015    -9.192517e-016
   7    8.422557e-016    3.330669e-016
   8    1.308801e-015    0.000000e+000
   9    1.229404e-015    6.106227e-016
10    1.185585e-015    9.192517e-016
11    6.785818e-016    1.998401e-015
12    1.045123e-015    2.983724e-015
13    -1.056958e-014    1.000000e+000
14    1.126707e-015    -2.744484e-015
15    8.422557e-016    -1.887379e-015

***************     実行結果のおわり    **************/

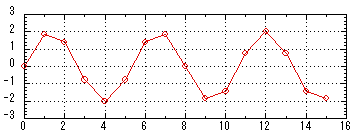
（データ番号16で0にもどるはず）
ファイル「timedomain.txt」
図４．１　１６サンプルで構成された時間領域波形

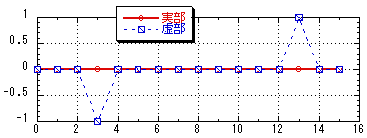
ファイル「spectrum.txt」
図４．２　１６サンプルで構成されたスペクトル

リスト３．１の関数maketimedomain()をリスト５．１のように変更すると図５．１の時間領域データと図５．２のスペクトルができる。時間領域波形は，「１６サンプルで構成された振幅２の４周期の余弦波」である。

リスト５．１　maketimedomain()の変更

void maketimedomain(double x[],int size)
{
    int i;
    for (i=0;i<size;i++) {
        x[i]=2.0*cos(4.0*(2*M_PI)*i/size);
    }
}

/**************     実行結果のはじまり    *************
ファイル「timedomain.txt」（時間領域データ）
   0    2.000000e+000
   1    3.231085e-015
   2    -2.000000e+000
   3    -9.249166e-015
   4    2.000000e+000
   5    1.659951e-014
   6    -2.000000e+000
   7    -2.217351e-014
   8    2.000000e+000
   9    2.952386e-014
10    -2.000000e+000
11    -3.332149e-014
12    2.000000e+000
13    4.067184e-014
14    -2.000000e+000
15    -4.802219e-014

ファイル「spectrum.txt」（複素数スペクトル）
（データは実部と虚部から成り立っている）
    0    -1.421254e-015    0.000000e+000
   1    -1.859266e-015    1.062160e-017
   2    -2.304348e-015    -1.373831e-016
   3    -4.027095e-015    2.564281e-017
   4    1.000000e+000    -1.267454e-014
   5    4.027095e-015    2.564281e-017
   6    2.304348e-015    -1.373831e-016
   7    1.859266e-015    1.062160e-017
   8    1.421254e-015    0.000000e+000
   9    1.859266e-015    -1.062160e-017
10    2.304348e-015    1.373831e-016
11    4.027095e-015    -2.564281e-017
12    1.000000e+000    1.267454e-014
13    -4.027095e-015    -2.564281e-017
14    -2.304348e-015    1.373831e-016
15    -1.859266e-015    -1.062160e-017

***************     実行結果のおわり    **************/

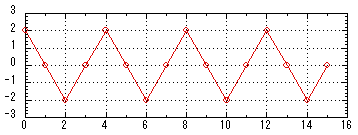
（データ番号16で+1.0にもどるはず。本来正弦波だが，
サンプル数が少ないので三角波のように見えている。）
ファイル「timedomain.txt」
図５．１　１６サンプルで構成された時間領域波形

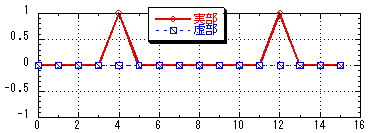
ファイル「spectrum.txt」
図５．２　１６サンプルで構成されたスペクトル

３，４，５で検討した高速フーリエ変換の３つの例をまとめてみよう。各スペクトルを見ると表６．１のようになる。

表６．１　高速フーリエ変換の３つの例のまとめ
時間領域波形の特徴	生成式	算出されたスペクトルの特徴
振幅1，sin波1波	x[i]=sin((2M_PI)i/size);	データ番号１虚部:-0.5 データ番号１5虚部:0.5 他は0.0（微小値）
振幅2，sin波3波	x[i]=2.0sin(3.0(2M_PI)i/size);	データ番号3虚部:-1.0 データ番号１3虚部:1.0 他は0.0（微小値）
振幅2，cos波4波	x[i]=2.0cos(4.0(2M_PI)i/size);	データ番号4実部:1.0 データ番号１2実部:1.0 他は0.0（微小値）

ここでよく見ると，スペクトルの図はデータ番号8に関して対称になっていることに気づく。正確に言うと実部はデータ番号8に関して線対称，虚部はデータ番号8に関して点対称である。実は，スペクトルデータは全データの前半のみ，意味があり，後半は前半の鏡像となっている。例では，データ番号0から7までが意味を持つ。前半だけで表６．１を書き直すと表６．２となる。

表６．２　高速フーリエ変換の３つの例のまとめ
時間領域波形の特徴	生成式	算出されたスペクトルの特徴
振幅1，sin波1波	x[i]=sin((2M_PI)i/size);	データ番号１虚部:-0.5 他は0.0（微小値）
振幅2，sin波3波	x[i]=2.0sin(3.0(2M_PI)i/size);	データ番号3虚部:-1.0 他は0.0（微小値）
振幅2，cos波4波	x[i]=2.0cos(4.0(2M_PI)i/size);	データ番号4実部:1.0 他は0.0（微小値）

表６．２より次のことがわかる。
（１）sin波のｉ波よりなる時間領域波形ではスペクトルのデータ番号iの虚部に値を持つ。
（２）cos波のｉ波よりなる時間領域波形ではスペクトルのデータ番号iの実部に値を持つ。
（３）sin波またはcos波の振幅値は0.5倍されてスペクトルの値になる。（逆にスペクトルの値を2倍するともとの正弦波の振幅となる）

さて，ここで，３つの例を，音の波形のサンプリングの例であると仮定してみよう。

そうすると，実際の周波数の関係は表６．３のようになる。周波数の有効範囲は700Hzまでとなる。そして

表６．３　サンプリング周波数1600Hzと仮定した場合の３つの例の音の周波数
時間領域波形の特徴	生成式	音の周期[秒]	周波数[Hz]
振幅1，sin波1波	x[i]=sin((2M_PI)i/size);	1/1600×16	100
振幅2，sin波3波	x[i]=2.0sin(3.0(2M_PI)i/size);	1/1600×16×1/3	300
振幅2，cos波4波	x[i]=2.0cos(4.0(2M_PI)i/size);	1/1600×16×1/4	400

一般化すると，サンプリング周波数fp[Hz]でサンプリングしたデータN個をデータブロックとして高速フーリエ変換した場合，

となる。周波数の有効範囲は0[Hz]から (N/2-1)×fs / N [Hz]までである。
このことは，時間領域データの波形中にサンプリング周波数の1/2未満の周波数成分しかありえないことを示す。
これは「ナイキストのサンプリング定理」そのものである。

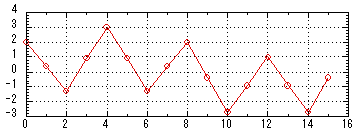
リスト３．１の関数maketimedomain()をリスト７．１のように変更すると2つの正弦波の合成波を高速フーリエ変換することになる。図７．１の時間領域データと図７．２のスペクトルができる。図７．１の時間領域データは，図３．１の時間領域データと図５．１の時間領域データを加え合わせてものであり，図７．２の周波数領域データは，図３．２の周波数領域データと図５．２の周波数領域データを加え合わせてものである。このように複数の正弦波が合成されてできた時間領域の波形は，スペクトルで見ると各周波数に分解して見ることができる。

リスト７．１　maketimedomain()の変更

void maketimedomain(double x[],int size)
{
    int i;
    for (i=0;i<size;i++) {
        x[i]=sin((2*M_PI)*i/size)+2.0*cos(4.0*(2*M_PI)*i/size);
    }
}

ファイル「timedomain.txt」
図７．１　１６サンプルで構成された時間領域波形

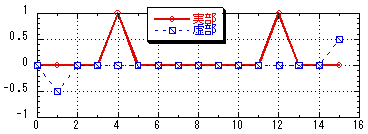
ファイル「spectrum.txt」
図７．２　１６サンプルで構成されたスペクトル

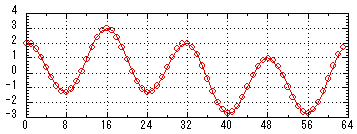
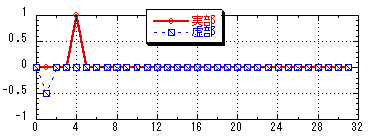
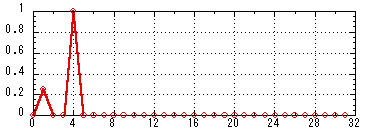
リスト８．１のように計算すると，パワースペクトルが計算できる。パワースペクトルは，スペクトル（複素数）の各値の絶対値の２乗のことで，スペクトル（複素数）の各値の「実部の２乗」+「虚部の２乗」で計算される。ここで1ブロックのサンプルデータ数を64とし，７と同じ時間領域波形とする。またこれより，周波数領域のデータは前半のみを表示する。実行結果は図８．１，８．２，８．３に示される。スペクトルは複素数でできており，直感的につかみにくいが，パワースペクトルは実数であり，どの周波数の成分がどれだけのパワーを持っているか考察するのに適している。「２．高速フーリエ変換の例」で示したDTMF音の分析は1024サンプルを1ブロックとしてこのパワースペクトルを求めたものである。
（図２．２のパワースペクトルも前半のみを示したものである。）
（パワースペクトルは本来パワースペクトル密度と呼ばれるのが正しい）

リスト８．１　64サンプルで構成された波形の高速フーリエ変換とパワースペクトル

#include <stdio.h>
#include <math.h>
#include "common.h"
#include "fftcore.h"
#define SIZE 64

void maketimedomain(double x[],int size)
{
    int i;
    for (i=0;i<size;i++) {
        x[i]=sin((2*M_PI)*i/size)+2.0*cos(4.0*(2*M_PI)*i/size);
    }
}

main()
{
    double timedomain[SIZE];    /*時間領域データ格納域*/
    dcomplex_t fftwork[SIZE];   /*複素数作業領域*/
    double powerspectrum[SIZE]; /*パワースペクトル格納域*/

/*FFTの初期化*/
initfft(SIZE);

    /*時間領域データの作成とファイル保存*/
    maketimedomain(timedomain,SIZE);
    savereal(timedomain,SIZE,"timedomain.txt");

    /*FFT作業の準備のため，時間領域データを複素数作業領域へ*/
    /*コピー*/
    real2cmp(timedomain,fftwork,SIZE);

    /*FFT（順方向フーリエ変換）*/
    /*作業領域fftworkの内容がスペクトルになる*/
    /*得られたスペクトルのファイルへの保存*/
    fft(1,fftwork,SIZE);
    savecmp(fftwork,SIZE/2,"spectrum.txt");

    /*パワースペクトルの計算とファイルへの保存*/
    makepower(fftwork,powerspectrum,SIZE,-1);
    savereal(powerspectrum,SIZE/2,"powerspectrum.txt");
}

ファイル「timedomain.txt」
図８．１　64サンプルで構成された時間領域波形

ファイル「spectrum.txt」
図８．２　64サンプルで構成されたスペクトルの前半32個

ファイル「spectrum.txt」
図８．３　64サンプルで構成されたスペクトルの前半32個

リスト９．１のプログラムの後半は逆フーリエ変換を示している。時間領域のデータ（comptimedomain.txt）が一度周波数領域に変換され，逆変換でふたたび時間領域のデータ（comptimedomain2.txt）になっている。この２つのデータがほとんど等しいことがわかる。

リスト３．１　１６サンプルで構成された正弦波の高速フーリエ変換

#include <stdio.h>
#include <math.h>
#include "common.h"
#include "fftcore.h"
#define SIZE 16

void maketimedomain(double x[],int size)
{
    int i;
    for (i=0;i<size;i++) {
        x[i]=sin((2*M_PI)*i/size)+2.0*cos(4.0*(2*M_PI)*i/size);
    }
}

main()
{
    double timedomain[SIZE]; /*時間領域データ格納域*/
    dcomplex_t fftwork[SIZE]; /*複素数作業領域*/

    /*FFTの初期化*/
    initfft(SIZE);

    /*時間領域データの作成とファイル保存*/
    maketimedomain(timedomain,SIZE);
    savereal(timedomain,SIZE,"timedomain.txt");

    /*FFT作業の準備のため，時間領域データを複素数作業領域へ*/
    /*コピーとファイル保存*/
    real2cmp(timedomain,fftwork,SIZE);
    savecmp(fftwork,SIZE,"comptimedomain.txt");

    /*FFT（順方向フーリエ変換）*/
    /*作業領域fftworkの内容がスペクトルになる*/
    /*得られたスペクトルのファイルへの保存*/
    fft(1,fftwork,SIZE);
    savecmp(fftwork,SIZE,"spectrum.txt");

    /*ここからがフーリエ逆変換*/
    fft(-1,fftwork,SIZE);
    savecmp(fftwork,SIZE,"comptimedomain2.txt");
}

/**************     実行結果のはじまり    *************
ファイル「comptimedomain.txt」（複素数化された時間領域データ）
   0    2.000000e+000    0.000000e+000
   1    3.826834e-001    0.000000e+000
   2    -1.292893e+000    0.000000e+000
   3    9.238795e-001    0.000000e+000
   4    3.000000e+000    0.000000e+000
   5    9.238795e-001    0.000000e+000
   6    -1.292893e+000    0.000000e+000
   7    3.826834e-001    0.000000e+000
   8    2.000000e+000    0.000000e+000
   9    -3.826834e-001    0.000000e+000
10    -2.707107e+000    0.000000e+000
11    -9.238795e-001    0.000000e+000
12    1.000000e+000    0.000000e+000
13    -9.238795e-001    0.000000e+000
14    -2.707107e+000    0.000000e+000
15    -3.826834e-001    0.000000e+000

ファイル「comptimedomain2.txt」（逆変換で得られた，複素数化された時間領域データ）
   0    2.000000e+000    0.000000e+000
   1    3.826834e-001    1.110223e-016
   2    -1.292893e+000    1.110223e-016
   3    9.238795e-001    -8.326673e-017
   4    3.000000e+000    0.000000e+000
   5    9.238795e-001    8.950111e-017
   6    -1.292893e+000    -1.431604e-016
   7    3.826834e-001    4.789245e-017
   8    2.000000e+000    0.000000e+000
   9    -3.826834e-001    -1.110223e-016
10    -2.707107e+000    -1.110223e-016
11    -9.238795e-001    8.326673e-017
12    1.000000e+000    0.000000e+000
13    -9.238795e-001    -8.950111e-017
14    -2.707107e+000    1.431604e-016
15    -3.826834e-001    -4.789245e-017
***************     実行結果のおわり    **************/

高速フーリエ変換について，その動作について解説した。高速フーリエ変換のアルゴリズムのプログラムへの実装は面倒で，難しい。この概説はアルゴリズムには触れず，FFTを関数としてとらえ，時間軸領域のデータと変換された周波数領域のデータ間の関係から，フーリエ変換で何ができるかに重点をおいた。