２． 使用環境
使用環境は２つあり，まったく同じプログラムでどちらの環境でも動作できるようにしている。
（１）UNIXでのコンパイルと実行（glutがインストールされている）
（２）WindowsマシンでのVisualC++でのコンパイルと実行（glutなどのインストールが必要）

参考　2.1　UNIXでのコンパイルのためのスクリプト（これをglgccのファイルにして実行可能にしておくと良い）

glgcc

#!/bin/sh if [ $# -eq 0 ] ; then    echo "Usage:  glgcc  file1.c [ file2.c .... ]"    exit fi src=$@ target=`echo $1  | sed ' s/\.c$// s/\.cpp$// s/\.cc$//'` if [ $1 = $target ] ; then    target=$1.out fi g++ $src -lglut -lGLU -lGL -lXmu -lXext -lX11 -ldl -lpthread -lm  -o $target

３． 最初のプログラム
３．１ 与えられた位置に点を打つプログラム　drawDot.cpp

「drawDot.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
main()中で以下の設定を確認しなさい。
glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB ); /*ダブルバッファ，RGBカラー*/
glutInitWindowPosition(100,100);
glutInitWindowSize(640,480);    /* windowの大きさを横640縦400に設定，*/
glutCreateWindow ("putPixel");  /*windowの名前*/
glClearColor(0.0, 0.0, 0.0, 0.0);   /*画面クリアの時は黒*/
gluOrtho2D(0., 640., 0.0, 480.0);  /*座標範囲をxは(0,640)，yは(0,400)に設定*/
  // Define the dimensions of the Orthographic Viewing Volume
glutDisplayFunc(display);        /*画面描画イベントの時に呼び出される関数名はdisplay*/
glutMainLoop();                 /*イベントループに突入*/

関数void setColor(float red,float green,float blue)は色の設定を行なう関数である。
関数void drawDot(int x,int y)は与えられた座標に点を打つ関数である。
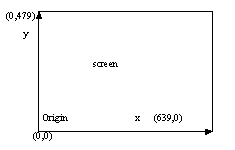
図３．１に座標軸，範囲の定義を示す。

ユーザは関数void userdraw()のみを変更して描画図形を変更することが出来る。

リスト3.1　drawDot.cpp

//drawDot //drawing dots with the given function drawDot() // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> void setColor(float red,float green,float blue) {     glColor3f(red, green, blue);    } void drawDot(int x,int y) {     glBegin(GL_POINTS);         glVertex2i(x, y);     glEnd(); } void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } void userdraw(void) {     setColor(1,1,1);     drawDot(50,400);     drawDot(50,350);     drawDot(50,300);     drawDot(100,400);     drawDot(100,350); } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("putPixel");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0.0, 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutDisplayFunc(display);     glutMainLoop();     return 0; }

３．２ 与えられた２点を線で結ぶプログラム　drawLine1.cpp

「drawLine1.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
与えられた２点を線で結ぶ関数void drawLine(int x1, int y1, int x2, int y2)は関数void drawDot(int x,int y)を用いて作られている。
図３．２に関数での作業状況を示す。

リスト3.2　drawLine1.cpp

//drawLine1 //showing two examples of the function drawLine() //void drawLine(int x1, int y1, int x2, int y2) // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> void setColor(float red,float green,float blue) {     glColor3f(red, green, blue);    } void drawDot(int x,int y) {     glBegin(GL_POINTS);         glVertex2i(x, y);     glEnd(); } void drawLine(int x1, int y1, int x2, int y2) {     int i, len, width = x2 - x1, height = y2 - y1;     float width_diff, height_diff;     if(abs(width) > abs(height)) len = abs(width);     else len = abs(height);     width_diff = (float)width / (float)len;     height_diff = (float)height / (float)len;     for(i = 0; i <= len; i++) {         drawDot((int)(x1 + i * width_diff+0.5),          (int)(y1 + i * height_diff+0.5));     } } void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } void userdraw(void) {     setColor(1,1,1);     drawLine(320+20,240+10,320+200,240+100);     drawLine(320+10,240+20,320+100,240+200);     drawLine(320-10,240+20,320-100,240+200);     drawLine(320-20,240+10,320-200,240+100);     drawLine(320-20,240-10,320-200,240-100);     drawLine(320-10,240-20,320-100,240-200);     drawLine(320+10,240-20,320+100,240-200);     drawLine(320+20,240-10,320+200,240-100); } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("Line 1");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0.0, 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutDisplayFunc(display);     glutMainLoop();     return 0; }

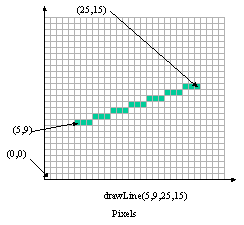図3.2 ドットで線を描く

参考　整数演算，しかも加算のみで直線を引くアルゴリズムがある。
Bresenhamの線分描画アルゴリズム　（マイコン組み込み機器のLCD上での描画などではよく使われる。）

３．３　動画を作る（１）　drawLine2.cpp

「drawLine2.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
main() 中にglutIdleFunc(display);で，アイドルイベント（待ちイベントがなくなった時に起こるイベント）の時呼び出される関数を設定。こ れにより，関数display()が自動的に何回も呼び出され，関数display()中で，描画画面がクリア（glClear( GL_COLOR_BUFFER_BIT);）され，関数userdraw()が呼び出され，描画画面を対象にuserdraw()が描画し，その後描画 画面と表示画面が交換（glutSwapBuffers();）される。すなわち関数userdraw()が間接的に何回も自動的に呼び出されることにな り，少しずつ異なる図形の描画を行なえばアニメーションになる。関数userdraw中にstatic変数tickを導入し，何回目の呼び出しかを数え， それに応じた描画をする。関数内static変数は，初期化（int x=123;と宣言された時の123の代入）はプログラム起動時に1回のみ行なわれ，関数の作業が終了しても値を保持し，次の関数呼び出しの時には，保持 された値を持っている変数である。

リスト3.3　drawLine2.cpp

//drawLine2 //showing the example of the function drawLine() //also showing animation with event driven method //A vertical line moves from left to right. // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> void setColor(float red,float green,float blue) {     glColor3f(red, green, blue);    } void drawDot(int x,int y) {     glBegin(GL_POINTS);         glVertex2i(x, y);     glEnd(); } void drawLine(int x1, int y1, int x2, int y2) {     int i, len, width = x2 - x1, height = y2 - y1;     float width_diff, height_diff;     if(abs(width) > abs(height)) len = abs(width);     else len = abs(height);     width_diff = (float)width / (float)len;     height_diff = (float)height / (float)len;     for(i = 0; i <= len; i++)         drawDot((int)(x1 + i * width_diff+0.5), (int)(y1 + i * height_diff+0.5)); } void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } void userdraw(void) {     static int tick=0;     int x;     x=tick%600+20;     setColor(1,1,1);     drawLine(x,400,x,50);     tick++; } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("Line 2");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0.0, 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display); // idle event call back     glutDisplayFunc(display);     glutMainLoop();     return 0; }

３． ４　動画を作る（２）　drawLine3.cpp

構造体point_tを利用した「drawLine3.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
関数void drawLine(int x1, int y1, int x2, int y2)を利用した，与えられた２点を線で結ぶ関数void drawLine(point_t p1,point_t p2)が作成されている。
このように同じソースファイル内に，引数は違うが，関数名が同じ関数をつくることを，関数の多重定義といい，C++での拡張である。

リスト3.4　drawLine3.cpp

//drawLine3 //showing another definition of the function drawLine() //void drawLine(point_t p1,point_t p2) //The example of function overloading //"structure point_t" is intruduced. //A line turns round counter clockwise. // T. Kosaka CS TNCT 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> typedef struct {     float x;     float y; } point_t; void setColor(float red,float green,float blue) {     glColor3f(red, green, blue);    } void drawDot(int x,int y) {     glBegin(GL_POINTS);         glVertex2i(x, y);     glEnd(); } void drawLine(int x1, int y1, int x2, int y2) {     int i, len, width = x2 - x1, height = y2 - y1;     float width_diff, height_diff;     if(abs(width) > abs(height)) len = abs(width);     else len = abs(height);     width_diff = (float)width / (float)len;     height_diff = (float)height / (float)len;     for(i = 0; i <= len; i++) {         drawDot((int)(x1 + i * width_diff+0.5),          (int)(y1 + i * height_diff+0.5));     } } void drawLine(point_t p1,point_t p2) {     drawLine((int)p1.x,(int)p1.y,(int)p2.x,(int)p2.y); } void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } void userdraw(void) {     static int tick=0;     point_t center={320,240};     point_t r;     r.x=200.*cos((float)tick*.01)+320;     r.y=200.*sin((float)tick*.01)+240;     setColor(1,1,1);     drawLine(center,r);     tick++; } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("Line 3");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0.0, 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display); // idle event call back     glutDisplayFunc(display);     glutMainLoop();     return 0; }

３．５　連続折れ線を描く　drawLine4.cpp　drawLine5.cpp

「drawLine4.cpp」「drawLine5.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
関数void drawLine(point_t p1,point_t p2)を利用した，与えられたｎ点を線で結ぶ関数void drawPolyline(point_t pnt[],int n)が作成されている。　ただしｎは有効点数

リスト3.5　drawLine4.cpp

//drawLine4 //showing the example of the function drawPolyline() //void drawPolyline(point_t pnt[],int n) //Two lines turn round like a clock hands. // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> typedef struct {     float x;     float y; } point_t; void setColor(float red,float green,float blue) {     glColor3f(red, green, blue);    } void drawDot(int x,int y) {     glBegin(GL_POINTS);         glVertex2i(x, y);     glEnd(); } void drawLine(int x1, int y1, int x2, int y2) {     int i, len, width = x2 - x1, height = y2 - y1;     float width_diff, height_diff;     if(abs(width) > abs(height)) len = abs(width);     else len = abs(height);     width_diff = (float)width / (float)len;     height_diff = (float)height / (float)len;     for(i = 0; i <= len; i++) {         drawDot((int)(x1 + i * width_diff+0.5),          (int)(y1 + i * height_diff+0.5));     } } void drawLine(point_t p1,point_t p2) {     drawLine((int)p1.x,(int)p1.y,(int)p2.x,(int)p2.y); } //n: number of points void drawPolyline(point_t pnt[],int n) {     int i;     for (i=0;i<n-1;i++) {         drawLine(pnt[i],pnt[i+1]);     } } void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } void userdraw(void) {     static int tick=0;     point_t pnt[3];     point_t center={320,240};     pnt[0].x=200.*cos(-(float)tick*.06+3.1415926535*.5)+320;     pnt[0].y=200.*sin(-(float)tick*.06+3.1415926535*.5)+240;     pnt[1]=center;     pnt[2].x=100.*cos(-(float)tick*.005+3.1415926535*.5)+320;     pnt[2].y=100.*sin(-(float)tick*.005+3.1415926535*.5)+240;     setColor(1,1,1);     drawPolyline(pnt,3);     tick++; } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("Line 4");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0.0, 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display);  // idle event call back     glutDisplayFunc(display);     glutMainLoop();     return 0; }

３．６　多角形を描く　drawPolygon.cpp

「drawPolygon.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
関数void drawLine(point_t p1,point_t p2)を利用して，与えられたｎ点でｎ角形を描く関数void drawPolygon(point_t pnt[],int n)が作成されている。ただし，ｎ角形の頂点の座標列は左回り（反時計回り）に定義することとする。

課題１
line4.cpp，line5.cppをもとに，自由な発想でプログラムdancinglines.cppを作成し，プログラムをwebで公開しなさい。
ただし，ファイル名はdancinglines.txtとし，画像もdancinglines.gifで公開しなさい。

参考１　描画画面のキャプチャ（ある瞬間の画面の保存）の方法 （１）画面を保存したいウィンドウの全部が見えるような配置にしておく。 　　　別のウインドウ（特に次で用いる端末エミュレータの画面）で一部が隠れないように 　　　しておく。 （２）端末エミュレータの画面で以下のコマンドを入力する。    camera  output.gif （３）カーソルが十字になったら、保存したいウィンドウをクリックする。 「output.gif」というファイルが出来たので，これをダブルクリックして画像を確認する。 ここで「output.gif」というのはファイル名なので，「XXXXXX.gif」という名前ならなんでも OKである。 参考２　Windowsマシンでの描画画面のキャプチャ（ある瞬間の画面の保存）の方法 （１）画面を保存したいウィンドウを最前面にしておく。 （２）「Ctrl」キーと「Alt」キーを押しながら「PrintScreen」キーを押すと，その瞬間の画像がコピーバッファにコピーされる。 （３）「Paint」などのアプリケーションを開き，ペーストする。 （４）保存の際に「ファイルの種類」をgifにして，ファイル名をつけて保存する。

課題１　自由な発想で線が動き回るプログラムdancinglines.c １．提出者名　4Jxx　高専太郎 ２．課題概要 ３．製作したプログラムソースdancinglines.c 　　#include ……. 　　： ４．まとめと感想  （１）苦労したポイント，理解してよかったポイント  （２）課題の難易度について  （３）提言  （４）その他

３．７　多角形を単色で塗りつぶし　fillpolygon.cpp

「fillpolygon.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
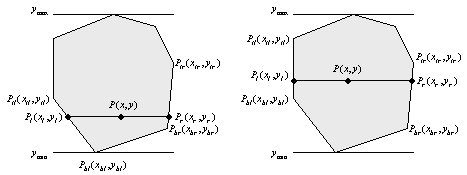
ｎ角形の頂点の座標列は左回りに定義してあることと，内分点の考え方で多角形の内部点をすべて求めて与えられた色で点を打っている。図3.3に塗りつぶす方法を示す。

リスト3.8　fillpolygon.cpp

//fillPolygon //showing the function of fillPolygon() //A filled square turns round counter clockwise. // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> typedef struct {     float x;     float y; } point_t; typedef struct {     float r;     float g;     float b; } color_t; void setColor(float red,float green,float blue) {     glColor3f(red, green, blue);    } void setColor(color_t col) {     glColor3f(col.r, col.g, col.b); } void drawDot(int x,int y) {     glBegin(GL_POINTS);         glVertex2i(x, y);     glEnd(); } void drawLine(int x1, int y1, int x2, int y2) {     int dx,dy,dx2,dy2,x,y,inc,c,tmp;     dx=0<=x2-x1?x2-x1:x1-x2;     dy=0<=y2-y1?y2-y1:y1-y2;     dx2=dx<<1;dy2=dy<<1;     if (dy<=dx) {         if (x2<x1) {             tmp=x1;x1=x2;x2=tmp;             tmp=y1;y1=y2;y2=tmp;         }         inc=0<=y2-y1?1:-1;         x=x1;y=y1;c=-dx;         drawDot(x,y);         for (x++;x<=x2;x++) {             c+=dy2;             if (0<=c) {c-=dx2;y+=inc;}             drawDot(x,y);         }     } else {         if (y2<y1) {             tmp=x1;x1=x2;x2=tmp;             tmp=y1;y1=y2;y2=tmp;         }         inc=0<=x2-x1?1:-1;         x=x1;y=y1;c=-dy;         drawDot(x,y);         for (y++;y<=y2;y++) {             c+=dx2;             if (0<=c) {c-=dy2;x+=inc;}             drawDot(x,y);         }     } } void drawLine(point_t p1,point_t p2) {     drawLine((int)p1.x,(int)p1.y,(int)p2.x,(int)p2.y); } //n: number of points void drawPolyline(point_t pnt[],int n) {     int i;     for (i=0;i<n-1;i++) {         drawLine(pnt[i],pnt[i+1]);     } } //n: number of vertices void drawPolygon(point_t pnt[],int n) {     int i;     for (i=0;i<n-1;i++) {         drawLine(pnt[i],pnt[i+1]);     }     drawLine(pnt[n-1],pnt[0]); } //p1．p2をs1：s2に内分する値を求める int interpolateInteger(int p1,int p2,float s1,float s2) {     if (s1<0.) s1=0.;     if (s2<0.) s2=0.;     if (s1+s2<1.) return p1;     return (int)((p1*s2+p2*s1)/(s1+s2)+.5); } //多角形ををcolorで塗りつぶす void fillPolygon(point_t pnt[],int num,color_t color) {     int top,bottom;     int topleft,topright,bottomleft,bottomright;     int ymax,ymin,xleft,xright;     int i,y,x;     //最上頂点と最下頂点の点番号を求める     top=0,bottom=0;     for(i=0;i<num;i++) {         if (pnt[top].y<pnt[i].y) top=i;         if (pnt[i].y<pnt[bottom].y) bottom=i;     }     ymax=(int)(pnt[top].y+0.5);     ymin=(int)(pnt[bottom].y+0.5);     bottomleft=bottomright=bottom;     topleft=(bottomleft-1+num)%num;     topright=(bottomright+1)%num;     setColor(color);     for (y=ymin;y<=ymax;y++) {//ｙの値を最上点から最下点に向けて変更する         if ((int)(pnt[topleft].y+0.5)<y) {//ｙが左側のある頂点より下になったら，2つの頂点番号を変更             bottomleft=topleft;             topleft=(bottomleft-1+num)%num;         }         if ((int)(pnt[topright].y+0.5)<y) {//ｙが右側のある頂点より下になったら，2つの頂点番号を変更             bottomright=topright;             topright=(bottomright+1)%num;         }         //ｙの高さで左側端点のｘ座標を求める         xleft=interpolateInteger(pnt[topleft].x,pnt[bottomleft].x,pnt[topleft].y-y,y-pnt[bottomleft].y);         //ｙの高さで右側端点のｘ座標を求める         xright=interpolateInteger(pnt[topright].x,pnt[bottomright].x,pnt[topright].y-y,y-pnt[bottomright].y);         for (x=xleft;x<=xright;x++) {//ｙの高さの横線を引く             drawDot(x,y);         }     } } void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } void userdraw(void) {     static int tick=0;     point_t pnt[4];     color_t color={1,0,1};     pnt[0].x=200.*cos(-(float)tick*.01)+320;     pnt[0].y=200.*sin(-(float)tick*.01)+240;     pnt[1].x=200.*cos(-(float)tick*.01+3.1415926535*.5)+320;     pnt[1].y=200.*sin(-(float)tick*.01+3.1415926535*.5)+240;     pnt[2].x=200.*cos(-(float)tick*.01+3.1415926535)+320;     pnt[2].y=200.*sin(-(float)tick*.01+3.1415926535)+240;     pnt[3].x=200.*cos(-(float)tick*.01+3.1415926535*1.5)+320;     pnt[3].y=200.*sin(-(float)tick*.01+3.1415926535*1.5)+240;     fillPolygon(pnt,4,color);     tick++; } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("fillPolygon");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0.0, 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display);  // idle event call back     glutDisplayFunc(display);     glutMainLoop();     return 0; }

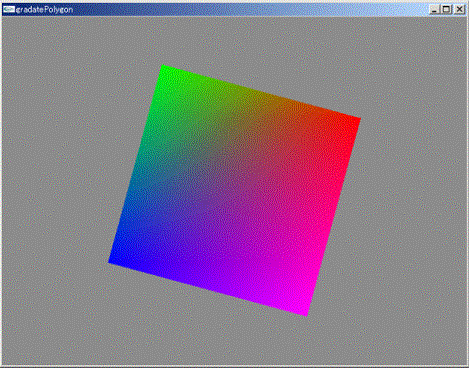
３．８　多角形のグラデーション塗りつぶし　gradatePolygon.cpp
（多角形の頂点の色だけ指定し，個々の内部点の色は徐々に変化するように整える。）

「gradatePolygon.cpp」をコンパイルして実行し，プログラム各部の役割を確認しなさい。
はじめに各辺上の点の色を，両端の頂点の色から内分点の考え方で決定し，線分と水平線の交点は2つあり，２つの交点の色から，水平線上の各点の色を内分点の考え方で決定する。

color_t型の構造体を導入している。
typedef struct {
    float r;
    float g;
    float b;
} color_t;

関数void setColor(color_t col)　の多重定義を導入している。
関数color_t interpolateColor(color_t c1,color_t c2,float s1,float s2)による色の補間を導入している。
関数void gradatePolygon(point_t pnt[],color_t col[],int num)によるグラデーション塗りつぶしを導入している。
この関数ではpoint_t pnt[],color_t col[],int numは，それぞれ頂点の配列，対応する頂点の色変数の配列，配列の有効要素数を表す。

リスト3.9　gradatePolygon.cpp

//gradatePolygon //showing the function of gradatePolygon() //A gradated square turns round counter clockwise. //The colors of the vertices are defined and colors //of inner points are interpolated. // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> typedef struct {     float x;     float y; } point_t; typedef struct {     float r;     float g;     float b; } color_t; void setColor(float red,float green,float blue) {     glColor3f(red, green, blue);    } void setColor(color_t col) {     glColor3f(col.r, col.g, col.b); } void drawDot(int x,int y) {     glBegin(GL_POINTS);         glVertex2i(x, y);     glEnd(); } void drawLine(int x1, int y1, int x2, int y2) {     int i, len, width = x2 - x1, height = y2 - y1;     float width_diff, height_diff;     if(abs(width) > abs(height)) len = abs(width);     else len = abs(height);     width_diff = (float)width / (float)len;     height_diff = (float)height / (float)len;     for(i = 0; i <= len; i++)         drawDot((int)(x1 + i * width_diff+0.5), (int)(y1 + i * height_diff+0.5)); } void drawLine(point_t p1,point_t p2) {     drawLine((int)p1.x,(int)p1.y,(int)p2.x,(int)p2.y); } //n: number of points void drawPolyline(point_t pnt[],int n) {     int i;     for (i=0;i<n-1;i++) {         drawLine(pnt[i],pnt[i+1]);     } } //n: number of vertices void drawPolygon(point_t pnt[],int n) {     int i;     for (i=0;i<n-1;i++) {         drawLine(pnt[i],pnt[i+1]);     }     drawLine(pnt[n-1],pnt[0]); } int interpolateInteger(int p1,int p2,float s1,float s2) {     if (s1<0.) s1=0.;     if (s2<0.) s2=0.;     if (s1+s2<1.) return p1;     return (int)((p1*s2+p2*s1)/(s1+s2)+.5); } color_t interpolateColor(color_t c1,color_t c2,float s1,float s2) {     color_t ret;     if (s1<0.) s1=0.;     if (s2<0.) s2=0.;     if (s1+s2<1.) {         ret=c1;     } else {         ret.r=(1./(s1+s2))*(c1.r*s2+c2.r*s1);         ret.g=(1./(s1+s2))*(c1.g*s2+c2.g*s1);         ret.b=(1./(s1+s2))*(c1.b*s2+c2.b*s1);     }     return ret; } void gradatePolygon(point_t pnt[],color_t col[],int num) {     int top,bottom;     int topleft,topright,bottomleft,bottomright;     int ymax,ymin,xleft,xright;     color_t colorleft,colorright,color;     int i,y,x;     top=0,bottom=0;     for(i=0;i<num;i++) {         if (pnt[top].y<pnt[i].y) top=i;         if (pnt[i].y<pnt[bottom].y) bottom=i;     }     ymax=(int)(pnt[top].y+0.5);     ymin=(int)(pnt[bottom].y+0.5);     bottomleft=bottomright=bottom;     topleft=(bottomleft-1+num)%num;     topright=(bottomright+1)%num;     for (y=ymin;y<=ymax;y++) {         if ((int)(pnt[topleft].y+0.5)<y) {             bottomleft=topleft;             topleft=(bottomleft-1+num)%num;         }         if ((int)(pnt[topright].y+0.5)<y) {             bottomright=topright;             topright=(bottomright+1)%num;         }         xleft=interpolateInteger(pnt[topleft].x,pnt[bottomleft].x,             pnt[topleft].y-y,y-pnt[bottomleft].y);         xright=interpolateInteger(pnt[topright].x,pnt[bottomright].x,             pnt[topright].y-y,y-pnt[bottomright].y);         colorleft=interpolateColor(col[topleft],col[bottomleft],             pnt[topleft].y-y,y-pnt[bottomleft].y);         colorright=interpolateColor(col[topright],col[bottomright],             pnt[topright].y-y,y-pnt[bottomright].y);         for (x=xleft;x<=xright;x++) {             color=interpolateColor(colorleft,colorright,x-xleft,xright-x);             setColor(color);             drawDot(x,y);         }     } } void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } void userdraw(void) {     static int tick=0;     point_t pnt[4];     color_t color[4]={         {1,0,1},{1,0,0},{0,1,0},{0,0,1}     };     pnt[0].x=200.*cos(-(float)tick*.01)+320;     pnt[0].y=200.*sin(-(float)tick*.01)+240;     pnt[1].x=200.*cos(-(float)tick*.01+3.1415926535*.5)+320;     pnt[1].y=200.*sin(-(float)tick*.01+3.1415926535*.5)+240;     pnt[2].x=200.*cos(-(float)tick*.01+3.1415926535)+320;     pnt[2].y=200.*sin(-(float)tick*.01+3.1415926535)+240;     pnt[3].x=200.*cos(-(float)tick*.01+3.1415926535*1.5)+320;     pnt[3].y=200.*sin(-(float)tick*.01+3.1415926535*1.5)+240;     gradatePolygon(pnt,color,4);     tick++; } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("gradatePolygon");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0.0, 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display);  // idle event call back     glutDisplayFunc(display);     glutMainLoop();     return 0; }

課題２
関数void gradatePolygon(point_t pnt[],color_t col[],int num) を用いて，回転する正五角形，正六角形を描き，グラデーション塗りつぶしを行ないなさい。gradatePentagon.cpp，gradateHexagon.cpp

提出は二つまとめて，gradatePolygons.txtでWeb上に公開しなさい。また２つの画像もgradatedPentagon.gifとgradatedHexagon.gifで公開しなさい。

 ４．　OpenGLの平面描画標準機能を用いた描画関数
こ こまではコンピュータグラフィックスの基礎を学ぶために，ドットの描画関数drawDot()のみがOpenGLの標準機能を用いた関数で，それ以外の描 画関数は関数drawDot()を呼び出して作ったものであった。しかし各描画関数はOpenGLの標準機能を用いた描画関数に置き換えることが出来る。

せっかくこれまでに作った関数drawDot，drawLine，drawPolyline，drawPolygon，fillPolygon，gradatePolygonは使うのをやめて，OpenGL環境が提供している方法で，これらの関数を作り直す。

「点の座標を表す構造体」「色を表す構造体」を残した上で，以下のヘッダーファイル「drawShape2D.h」に示されるように，関数を置き換える。

リスト４．１　drawShape2D.h

typedef struct {     float x;     float y; } point2D_t; typedef struct {     float r;     float g;     float b; } color_t; void setColor(color_t col); void drawDot(point2D_t pt); void drawLine(point2D_t p1,point2D_t p2); void drawLine(float x1,float y1,float x2,float y2); //n: number of points void drawPolyline(point2D_t pnt[],int n); //n: number of vertices void drawPolygon(point2D_t pnt[],int n); // The function fillPolygon can fills only convex polygons //n: number of vertices void fillPolygon(point2D_t pnt[],int n,color_t color); // The function gradatePolygon can fills only convex polygons // The vertices will be painted with corresponding given colors. // The points inside the polygon will be painted with the mixed color. //n: number of vertices void gradatePolygon(point2D_t pnt[],color_t col[],int num);

また，プログラム本体「drawShape2D.cpp」は次のようになる。

リスト４．２　drawShape2D.cpp

////////////// OpenGL drawShape for 2D Functions ver 1 ///////////////// #include <GL/glut.h> #include "drawShape2D.h" void setColor(color_t col) {     glColor3f(col.r, col.g, col.b); } void drawDot(point2D_t pt) {     glBegin(GL_POINTS);         glVertex2f(pt.x, pt.y);     glEnd(); } void drawLine(point2D_t p1,point2D_t p2) {     glBegin(GL_LINES);         glVertex2f(p1.x, p1.y);         glVertex2f(p2.x, p2.y);     glEnd(); } void drawLine(float x1,float y1,float x2,float y2) {     glBegin(GL_LINES);         glVertex2f(x1, y1);         glVertex2f(x2, y2);     glEnd(); } //n: number of points void drawPolyline(point2D_t pnt[],int n) {     int i;     glBegin(GL_LINE_STRIP);         for (i=0;i<n;i++) {             glVertex2f(pnt[i].x, pnt[i].y);         }     glEnd(); } //n: number of vertices void drawPolygon(point2D_t pnt[],int n) {     int i;     glBegin(GL_LINE_LOOP);         for (i=0;i<n;i++) {             glVertex2f(pnt[i].x, pnt[i].y);         }     glEnd(); } // The function fillPolygon can fills only convex polygons //n: number of vertices void fillPolygon(point2D_t pnt[],int n,color_t color) {     int i;     setColor(color);     glBegin(GL_POLYGON);         for (i=0;i<n;i++) {             glVertex2f(pnt[i].x, pnt[i].y);         }     glEnd(); } // The function gradatePolygon can fills only convex polygons // The vertices will be painted with corresponding given colors. // The points inside the polygon will be painted with the mixed color. //n: number of vertices void gradatePolygon(point2D_t pnt[],color_t col[],int num) {     int i;     glBegin(GL_POLYGON);         for (i=0;i<num;i++) {             setColor(col[i]);             glVertex2f(pnt[i].x, pnt[i].y);         }     glEnd(); }

プログラム例「primitives.cpp」を「drawShape2D.cpp」，「drawShape2D.h」とともにコンパイルして実行し，プログラムの各部の働きを確認しなさい。
次の２つのプログラムでは，main()中の設定によりウインドウの中央が原点になっている。

「2Dfigures.cpp」を「drawShape2D.cpp」，「drawShape2D.h」とともにコンパイルして実行し，プログラムの各部の働きを確認しなさい。
「morphing.cpp」を「drawShape2D.cpp」，「drawShape2D.h」とともにコンパイルして実行し，プログラム各部の働きについて確認しなさい。

課題　３
（１）「drawShape2D.cpp」中にあるすべての関数の役割を説明しなさい。
（２）「morphing.cpp」を変更して，自分で作成したモーフィングプログラムにしなさい。
課題はWEB公開とし，ファイル名「morphingObjects.txt」で公開しなさい。なお画像も「morphingObjects.gif」で公開しなさい。

５．　マウスとキーボードの利用
マウスとキーボードの利用はコンピュータグラフィックスとは関係ないが，これらが使えると，プログラミングの範囲が広がるため紹介する。
この章は「drawShape2D.cpp」の描画関数を使用することとし，コンパイル時には「drawShape2D.cpp」を含めてコンパイルすることを前提とする。

５．１　マウスのクリックによる連続線分の描画　MouseButtonS.cpp

「MouseButtonS.cpp」をコンパイルして実行し，プログラムの各部の働きを確認しなさい。
main()中で「glutMouseFunc(onMouseButton);」のように書くことで，マウスボタンの状態が変化したときに呼び出される関数名を設定する。
マウスボタンの状態が変化したときに呼び出される関数「void onMouseButton(int button, int state, int x, int y_inv)」の引数の数と順番は自分で変更してはいけない。（引数の変数名の変更はよい）
関数「void onMouseButton(int button, int state, int x, int y_inv)」では座標をグローバル変数に覚えさせるだけで，描画は関数「userdraw()」で行なう。

リスト５．１　MouseButtonS.cpp

//MouseButtonS //  Drawing polyline //  saving current point // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> #include "drawShape2D.h" void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } int NumberofPoints; point2D_t PointBuffer[4096]={{0,0}}; //マウスボタンが押された時に呼び出される関数 void onMouseButton(int button, int state, int x, int y_inv) {     int y=480-y_inv-1;  // device coordinate -> view coordinate     switch (button) {     case GLUT_LEFT_BUTTON:         if (state == GLUT_UP && NumberofPoints!=4096) {             PointBuffer[NumberofPoints].x=x;             PointBuffer[NumberofPoints].y=y;             NumberofPoints++;         }         break;     case GLUT_MIDDLE_BUTTON:         // do nothing         break;     case GLUT_RIGHT_BUTTON:         // do nothing         break;     default:         break;     } } void userdraw(void) {     int i;     color_t white={1.,1.,1.};     setColor(white);     if (1<NumberofPoints) {         for(i=0;i<NumberofPoints;i++) {             drawPolyline(PointBuffer,NumberofPoints);         }     } } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("MouseButtonS  !!! Click the screen with the mouse. !!!");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0., 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display); // idle event call back     glutDisplayFunc(display);     glutMouseFunc(onMouseButton);   // mouse button event call back     NumberofPoints=0;     glutMainLoop();     return 0; }

５．２　マウスのドラッグによる連続線分の描画　MouseMotion.cpp

「MouseMotion.cpp」をコンパイルして実行し，プログラムの各部の働きを確認しなさい。
main()中で「glutMotionFunc(onDrag);」のように書くことで，マウスが移動したときに呼び出される関数名を設定する。

リスト５．２　MouseMotion.cpp

//MouseMotion //  Drawing polyline // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> #include "drawShape2D.h" void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } int NumberofPoints=1; point2D_t PointBuffer[4096]={{0,0}}; int drag=0; point2D_t CurrentPoint; void onMouseButton(int button, int state, int x, int y_inv) {     int y=480-y_inv-1;  // device coordinate -> view coordinate     switch (button) {     case GLUT_LEFT_BUTTON:         if (state == GLUT_UP && NumberofPoints!=4096) {             PointBuffer[NumberofPoints].x=x;             PointBuffer[NumberofPoints].y=y;             NumberofPoints++;             drag=0;         }         break;     case GLUT_MIDDLE_BUTTON:         // do nothing         break;     case GLUT_RIGHT_BUTTON:         // do nothing         break;     default:         break;     } } //マウスがドラッグされた時に呼び出される関数 void onDrag(int x, int y_inv) {     int y=480-y_inv-1;  // device coordinate -> view coordinate     drag=1;     CurrentPoint.x=x;     CurrentPoint.y=y; } void userdraw(void) {     int i;     color_t white={1.,1.,1.};     color_t cyan={0.,1.,1.};     setColor(white);     if (1<NumberofPoints) {         for(i=0;i<NumberofPoints;i++) {             drawPolyline(PointBuffer,NumberofPoints);         }     }     setColor(cyan);     if (0<NumberofPoints && drag==1) {         drawLine(PointBuffer[NumberofPoints-1],CurrentPoint);     } } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("MouseMotion  !!! Drag the pointer on the screen with the mouse. !!!");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0., 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display); // idle event call back     glutDisplayFunc(display);     glutMouseFunc(onMouseButton);   // mouse button event call back     glutMotionFunc(onDrag); // mouse drag event call back     glutMainLoop();     return 0; }

５．３　キーボード入力　hitKey.cpp　 hitKeyM.cpp

「hitKey.cpp」をコンパイルして実行し，プログラムの各部の働きを確認しなさい。
「hitKeyM.cpp」をコンパイルして実行し，プログラムの各部の働きを確認しなさい。

main()中で「glutKeyboardFunc(onKeyboard);」のように書くことで，キーボードのキーが押されたときに呼び出される関数名を設定する。

リスト５．３　hitKey.cpp

//hitKey //  Drawing a circle at the position of the pointer when key 'A' is hit. //  Drawing a square at the position of the pointer when key 'B' is hit. //  glutKeyboardFunc(onKeyboard); // keyboard event call back //  void onKeyboard(unsigned char key, int x, int y_inv) // coskx TNCT 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> #include "drawShape2D.h" #ifndef M_PI #define M_PI 3.141592653589793 #endif void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } unsigned int GlobalTick=1000; point2D_t CurrentPoint; int circle; void onKeyboard(unsigned char key, int x, int y_inv) {     int y=480-y_inv-1;  // device coordinate -> view coordinate     switch (key) {     case 'A':     case 'a':         GlobalTick=10;         CurrentPoint.x=x;         CurrentPoint.y=y;         circle=1;         break;     case 'B':     case 'b':         GlobalTick=10;         CurrentPoint.x=x;         CurrentPoint.y=y;         circle=0;         break;     default:         break;     } } void userdraw(void) {     float r;     int num;     int i;     color_t cyan={0.,1.,1.};     point2D_t p[600];     if (GlobalTick<400) {         r=GlobalTick;         if (circle==1) {             num=GlobalTick/20+30;         } else {             num=4;         }         for (i=0;i<num;i++) {             p[i].x=r*cos(2.*M_PI*i/num)+CurrentPoint.x;             p[i].y=r*sin(2.*M_PI*i/num)+CurrentPoint.y;         }         setColor(cyan);         drawPolygon(p,num);     }     GlobalTick++;     if (50000<GlobalTick) GlobalTick=1000; } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("hitKey  !!! Push 'A' or 'B' key with the mouse moving. !!!");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0., 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display); // idle event call back     glutDisplayFunc(display);     glutKeyboardFunc(onKeyboard); // keyboard event call back     glutMainLoop();     return 0; }

リスト５．４　hitKeyM.cpp

//hitKeyM //  Drawing a circle at the position of the pointer when key 'A' is hit. // T. coskx 2001 #include <stdio.h> #include <math.h> #include <GL/glut.h> #include "drawShape2D.h" #ifndef M_PI #define M_PI 3.141592653589793 #endif void userdraw(void); void display(void) {     glClear( GL_COLOR_BUFFER_BIT);     userdraw();     glutSwapBuffers(); } unsigned int GlobalTick[40]={     1000,1000,1000,1000,1000,     1000,1000,1000,1000,1000,     1000,1000,1000,1000,1000,     1000,1000,1000,1000,1000,     1000,1000,1000,1000,1000,     1000,1000,1000,1000,1000,     1000,1000,1000,1000,1000,     1000,1000,1000,1000,1000 }; point2D_t CurrentPoint[40]; void onKeyboard(unsigned char key, int x, int y_inv) {     int y=480-y_inv-1;  // device coordinate -> view coordinate     int k;     switch (key) {     case 'A':     case 'a':         for (k=0;k<40;k++) {             if (400<GlobalTick[k]) {                 GlobalTick[k]=10;                 CurrentPoint[k].x=x;                 CurrentPoint[k].y=y;                 break;             }         }         break;     default:         break;     } } void userdraw(void) {     float r;     int num;     int i,k;     color_t col;     point2D_t p[600];     for (k=0;k<40;k++) {         if (GlobalTick[k]<400) {             r=GlobalTick[k];             num=GlobalTick[k]/20+30;             for (i=0;i<num;i++) {                 p[i].x=r*cos(2.*M_PI*i/num)+CurrentPoint[k].x;                 p[i].y=r*sin(2.*M_PI*i/num)+CurrentPoint[k].y;             }             col.r=((int)CurrentPoint[k].x%256)/128.0+0.2;             col.g=((int)CurrentPoint[k].y%256)/128.0+0.2;             col.b=((int)(CurrentPoint[k].x+CurrentPoint[k].y)%256)/128.0+0.2;             setColor(col);             drawPolygon(p,num);         }         GlobalTick[k]++;         if (50000<GlobalTick[k]) GlobalTick[k]=1000;     } } int main(int argc, char **argv) {     glutInit(&argc,argv);     glutInitDisplayMode ( GLUT_DOUBLE | GLUT_RGB );     glutInitWindowPosition(100,100);     glutInitWindowSize(640,480);     glutCreateWindow ("hitKeyM  !!! Push 'A' key with the mouse moving. !!!");     glClearColor(0.0, 0.0, 0.0, 0.0);     gluOrtho2D(0., 640., 0., 480.0);       // Define the dimensions of the Orthographic Viewing Volume     glutIdleFunc(display); // idle event call back     glutDisplayFunc(display);     glutKeyboardFunc(onKeyboard);   // keyboard event call back     glutMainLoop();     return 0; }

課題　４
キーボード，マウスを使い，簡単な動画またはゲームを作りなさい。
課題はWEB公開とし，ファイル名「MouseAndKey.txt」で公開しなさい。なお画像も「MouseAndKey.gif」で公開しなさい。

６．　平面図形の座標変換
６．１　座標変換の数学的表現
平 面図形はすべての平面図形の頂点を座標で表すことにより定義される。例えば直角三角形のあるものは(0,0)，(3,0)，(0,4)で定義される。この 図形を平行移動させるにはすべての頂点座標を平行移動してから各点を結べばよい。この図形を原点中心に回転させるにはすべての頂点座標を原点のまわりに回 転させてから各点を結べばよい。このように座標を変更することを座標変換という。座標変換の基本的なものとして，平行移動，回転，拡大（縮小，対称移動） がある。例として，直線（線分）の平行移動のようすを図6.1に示す。

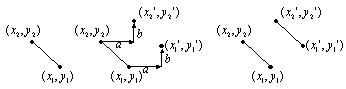図６．１　線の平行移動

（１）平行移動（translation）
点(x,y)を右方向にa，上方向にb移動すると新しい座標(x',y')は図6.2のように表される。また点(x,y)を固定し，座標軸を左方向にa，下方向にb移動しても同じ変換式となる。

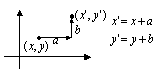図６．２　点の平行移動

（２）回転(rotation)
点(x,y)を原点中心に反時計回りにθ回転させると新しい座標(x',y')は図6.3のように表される。また点(x,y)を固定し，座標軸を時計回りにθ回転させても同じ変換式となる。

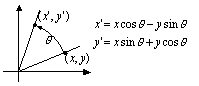図６．３　点の回転

（３）拡大（scaling）
点(x,y)を点(fx x,fy y)に移動する。同様な変換をすべての点について行なうと，もし1<fx=fyならば図形が拡大される。もしfx=fy<1ならば図形は縮小 される。さらにfx=1，fy=-1ならばx軸対称移動となり，fx=-1，fy=1ならばy軸対称移動，fx=fy=-1ならば原点対称移動になる

６．２　変換行列を用いた座標変換
平行移動と回転，拡大を統一的に扱うため，同次座標系（Homogeneous coordinate）を用いる。
（１）平行移動　（translation）
　
（２）回転　（rotation）
　 
（３）拡大　（scaling）
　

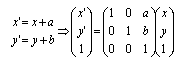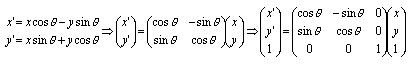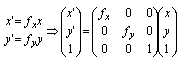６．３　座標の連続変換
ある点の座標(x,y)を回転移動して(x',y')にしてからさらに平行移動して(x",y")にする変換を連続変換（複合変換）と呼ぶ。この連続変換は

と表されるので

と書くことが出来，

とすると

と記述される。なおこの変換は変換の順番を変更すると変換結果が異なり，行列演算では交換法則が成り立たないことに対応している。

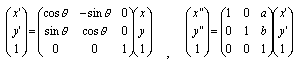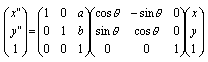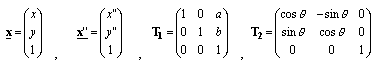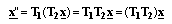６．４　変換行列を用いたプログラミング
プログラミングは構造体で点の座標と変換行列を扱う方法とC++のクラスで点の座標と変換行列を扱う方法がある。
Webで両方の記述を用いたプログラム例を与えるので比較してみよう。

６，４，１　構造体で点の座標と変換行列を扱うプログラミング
「ef.cpp」：「drawtools2D.cpp」「drawtools2D.h」とともにコンパイルする。
「rotef.cpp」：「drawtools2D.cpp」「drawtools2D.h」とともにコンパイルする。連続変換の例となっている。
この２つのプログラムをコンパイルして実行しなさい。

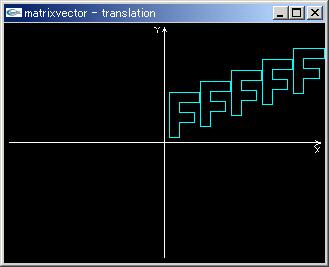プログラム　ef.cpp 「drawtools2D.cpp」とともにコンパイルすること

ポイント説明
関数matrix2D_t multiply(matrix2D_t a,matrix2D_t b)は行列同士の積を計算する関数で，戻り値は積を表す行列である。
使い方は2つの行列を表す変数mat1,mat2と積行列を表すproductがあったとすると

    matrix2D_t mat1,mat2,product;
     ：
    product= multiply(mat1,mat2);

のようになる。
次の表現も演算子「*」の再定義であるが，関数と同様に扱う。

matrix2D_t operator * (matrix2D_t a, matrix2D_t b)
{
    matrix2D_t c;//c=a*b
    int i,j,k;
    for (i=0;i<3;i++) for (j=0;j<3;j++) {
        c.m[i][j]=0;
        for (k=0;k<3;k++) c.m[i][j]+=a.m[i][k]*b.m[k][j];
    }
    return c;
}

この演算子「*」の使い方は，
使い方は2つの行列を表す変数mat1,mat2と積行列を表すproductがあったとすると

    matrix2D_t mat1,mat2,product;
     ：
    product= mat1*mat2;

のようになる。通常の関数と異なり，引数は演算子「*」をはさむように，前後に２つとる関数であると解釈すると良い。この演算子を用いることで，行列の積を数学で扱うように*で表すことができ，便利である。
同様に
vector2D_t multiply(matrix2D_t a, vector2D_t b);
vector2D_t operator * (matrix2D_t a, vector2D_t b);
も「行列×ベクトル」の積を求める関数となっている。

課題　５
ファイル「drawtools2D.cpp」にあるすべての関数の役割を説明しなさい。
提出はWeb公開とし，ファイル名は「drawtools2D.txt」としなさい。

６．４．２　C++のクラスで点の座標と変換行列を扱うプログラミング
「efwithclass.cpp」：「CGCore2D.cpp」「CGCore2D.h」とともにコンパイルする。
「rotefwithclass.cpp」：「CGCore2D.cpp」「CGCore2D.h」とともにコンパイルする。連続変換の例となっている。
「drawtools2D.cpp」では演算子「*」が再定義され
行列=行列*行列
ベクトル=行列*ベクトル　（座標=行列*座標）
の2つが作られていた。
「CGCore2D.cpp」では演算子「*」および演算子「=」がさらに再定義され
点列=行列*点列　（点列の個々の点に対して行列との積を作る）
多角形の頂点列=行列*多角形の頂点列　（多角形の頂点列の個々の点に対して行列との積を作る）
も使えるようになっている。

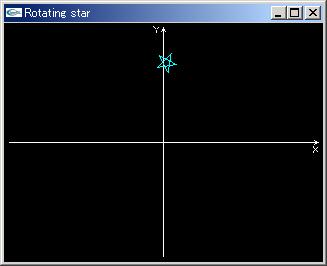プログラム　rotatingStar.cpp 「CGCore2D.cpp」とともにコンパイルすること

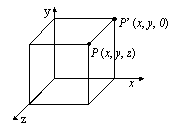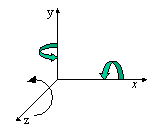図７．１　右手座標系	図７．２　軸周り回転の正方向

（１）平行移動　（translation）
 

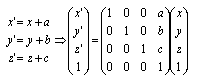（２）回転　（rotation）
回転はx軸周り，y軸周り，z軸周りの３つ がある。各軸周りの回転では，軸の正方向にねじを置き，ねじが軸の正方向に進むように回転させる向きを正の回転方向とする。例えば，ｚ軸の正方向にねじを 置き，ねじがｚ軸の正方向に進むように回転させる向き（xｙ平面で反時計回り）を正の回転方向とする。（図7.2参照）

（２．１）ｚ軸周りの回転
   

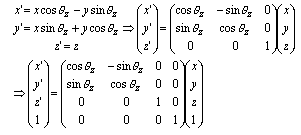（２．２）x軸周りの回転
  

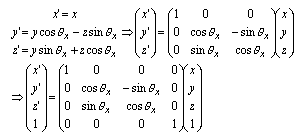（２．３）y軸周りの回転
 

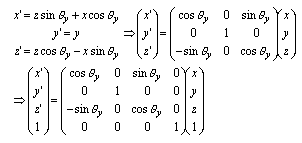（３）拡大　（scaling）
 

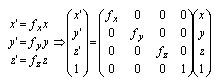７．２　xy平面への射影
空間図 形を画面上に表示するには，3次元−2次元変換を行なう。画面をxy平面に見立て，点P(x,y,z)からxy平面に垂線をたらした点を P'(x,y,0)とする。点PをP'に移すことにより，平面上に空間図形を描くことが出来る。例えば空間上の三角形 (2,6,4)-(5,4,8)-(2,3,1)はxy平面上の三角形(2,6,0)-(5,4,0)-(2,3,0)すなわち三角形 (2,6)-(5,4)-(2,3)となる。

７．３　ティルティング変換と各種変換
空 間図形を表現する時，斜め上から見ると，図形を把握しやすい。そこで，図形をy軸まわりに負の方向に適当な角度回転させ，次にx軸まわりに正の方向に適当 な角度回転させる変換を考える。この変換は，視点をy軸まわりに正の方向に適当な角度回転させ，次にx軸まわりに負の方向に適当な角度回転させる変換と同 じである。この変換はティルティング変換（図7.3参照）と呼ばれる。

図７．３　ティルティング変換

プログラム「tilting.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。ティルティングの手順が示される。
プログラム「ef3D.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。基本三次元変換の例が示される。

プログラム「ef3D.cpp」

プログラム「rotDemo.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。３つの軸周りの変換と正の回転方向が示される。
プログラム「rollingPentagon.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。複合変換例が示される。

プログラム「rollingPentagon.cpp」

プログラム「rollingPentagon2.cpp」を「drawtools3D.cpp」「drawtools3D.h」 とともにコンパイルして実行しなさい。面に表裏をつけて表示している。多角形の頂点をP0,P1,P2,P3,…,Pnとし，xy平面状で座標定義を反時 計回りにしたとすると，ベクトルP1-P0とP2-P0の外積をつくると法線ベクトルが得られ，そのｚ成分が正なら表面がz軸正側に向いており（表面がz 軸正側から見える），負なら裏面がz軸正側に向いている（裏面がz軸正側から見える），と考えられる。（図7.4参照）

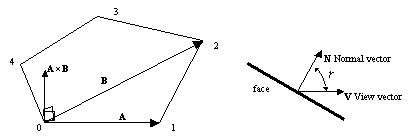図７．４　法線ベクトルと面の表裏

７．４　透視図（遠近感の表し方）
視点に近いものほど大きく，視点から遠いものほど小さく見えるようにする投影方法がある。
視点をｚ軸上ｚeに置くと図７．５のような変換を行なえばよい。

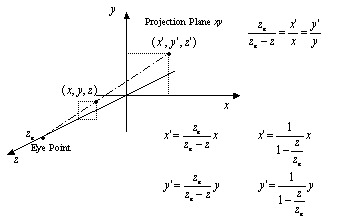図７．５　法線ベクトルと面の表裏

透視変換の変換行列と同次ベクトル化
 

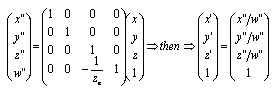プログラム「rollingPentagon3.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。遠近感表現がされている。これは透視変換行列関数
matrix3D_t perspectiveMTX(float eyelength)
と同次ベクトル化関数
vector3D_t homogenizeVector(vector3D_t vec)
の利用で実現されている。
透視変換行列は変換行列の先頭（変換作業においては最後）に置けれなければならない。

７．５　光と色の効果
光の効果は，（１）散乱反射（２）光点反射（３）環境光反射の３つがあり。このうち「散乱反射」「環境光反射」のみを考えるモデルは「ランバーモデル」，「散乱反射」「光点反射」「環境光反射」の３つを考えるモデルは「フォンモデル」と呼ばれる。
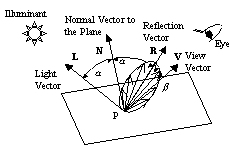
ある面の色は，その面の法線ベクトル・光源の方向ベクトル・視点の方向ベクトル（この３つのベクトルの大きさは１である。図７．６参照）とその面の属性としての色から計算される。

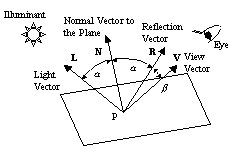図７．６　面の法線ベクトル・光源の方向ベクトル・視点の方向ベクトル

（１）散乱反射　Diffuse Scattering
散乱反射は，面の法線ベクトルと光源ベクトルの角度のみによりその面の明るさが決まり，視点ベクトルの向きには依存しない反射である。（図７．７参照）
 

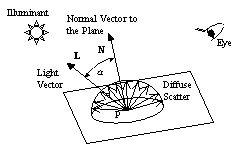図７．７　散乱反射　Diffuse Scattering

 
（２）光点反射　Specular Reflection
光点反射は，自動車のボディに太陽が反射するように，面のどこかにハイライト部が生ずる反 射である。面の法線ベクトルに対して入射角反射角が等しくなるような方向に光源方向ベクトルと反射方向ベクトルが存在し，反射方向ベクトル周辺に強い反射 が存在する。（図７．８参照） 

図７．８　光点反射　Specular Reflection

（３）環境光反射　Ambient
太陽が直接照らしていなくても，空の明るさや周囲の明るさにより，ものが見える原理である。面の法線ベクトルによらず，一定値の明るさを与える。

プログラム「rollingPentagon4.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。

課題　７
ファイル「drawtools3D.cpp」にあるすべての関数の役割を説明しなさい。
提出はWeb公開とし，ファイル名は「drawtools3D.txt」としなさい。

課題　８
ファイル「drawtools3D.cpp」を用いて，遠近感があり，かつ光の効果のある環境でｎ角形が適当な運動しているアニメーションプログラム「drawPolygonIn3D.cpp」を作りなさい。なお多角形（polygon）の描画（fillおよびgradate）では，凸多角形（convex polygon，どの内角も180度未満）のみ扱うことができるが，関数fillConcavePolygon()，gradateConcavePolygon()を自分で作って凹多角形を描いても良い。
提出はWeb公開とし，ファイル名は「drawPolygonIn3D.txt」としなさい。また画像ファイルは「drawPolygonIn3D.gif」としなさい。

８．　多面体の表現と曲面で構成される立体の表現
８．１　多面体の表現
立方体，直方体，三角柱，正八面体などは平面で囲まれた多面体（polyhedron）である。多面体を定義するには，
（１）すべての頂点の座標を確定し
（２）各面がどの頂点によって構成されているか
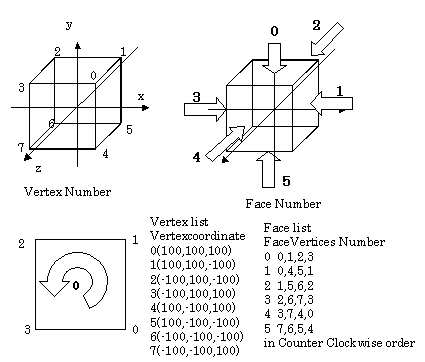
を設定すればよい。たとえば立方体の場合は図８．１のようにする。
（１）頂点は全部で8個あるので，適当に0から7までの番号を付ける。
（２）頂点番号0の座標は(100,100,100)，頂点番号1の座標は(100,100,-100)のようにすべての座標を定める。
（３）面は全部で6こあるので面番号を0から5まで適当に付ける
（４） 各面を構成する頂点番号を確定する。たとえば面番号0を構成する頂点番号は(0,1,2,3)，面番号１を構成する頂点番号は(0,4,5,1)，面番号 2を構成する頂点番号は(1,5,6,2)．．．のように行なう。ここで頂点番号の並べ方が重要で，面を外側から見て反時計回りに並べる必要がある。これ は，面の法線ベクトルを求めるときにベクトルの外積を用いるが，法線が多面体の外側を向くようにするためである。

図８．１ 立体の記述　（立方体の例）

プログラム「cube.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。
次の構造体で多面体を表現している。関数makeCube()により，立方体を表現する構造体を生成している。ある面が見えるか見えないかは面の法線ベクトルを検査して判断している。透視変換，フォンモデルによる面の色の設定は前節の方法を用いている。

typedef struct {
    int NumberofVertices; //in the face
    short int pnt[32];
} face_t;
typedef struct {
    int NumberofVertices; //of the object
    point3D_t pnt[100];
    int NumberofFaces; //of the object
    face_t fc[32];
} polyhedron_t;

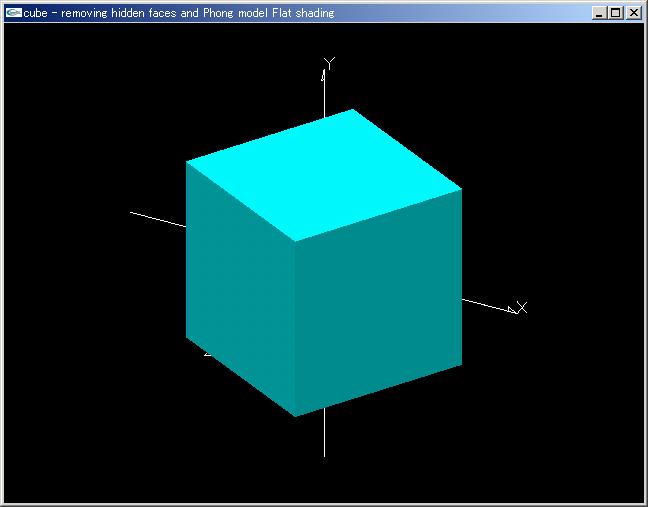
プログラム「cube.cpp」

正十二面体表示アニメーションプログラム「dodecahedron.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。

付図　正十二面体の頂点と面の記述

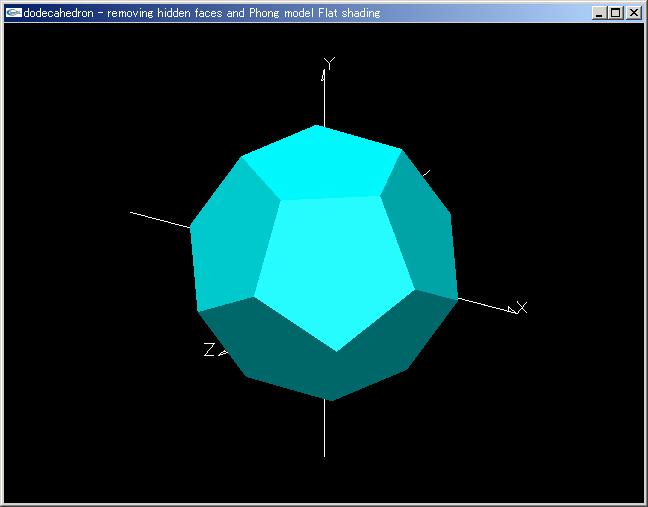
正十二面体表示アニメーションプログラム「dodecahedron.cpp」

正二十面体表示アニメーションプログラム「icosahedron.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。

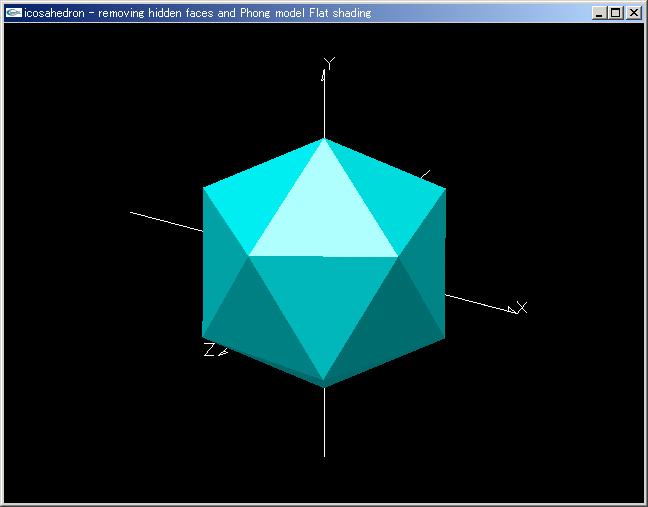正二十面体表示アニメーションプログラム「icosahedron.cpp」

正十二面体と正二十面体が踊るアニメーションプログラム「polyhedrons.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。

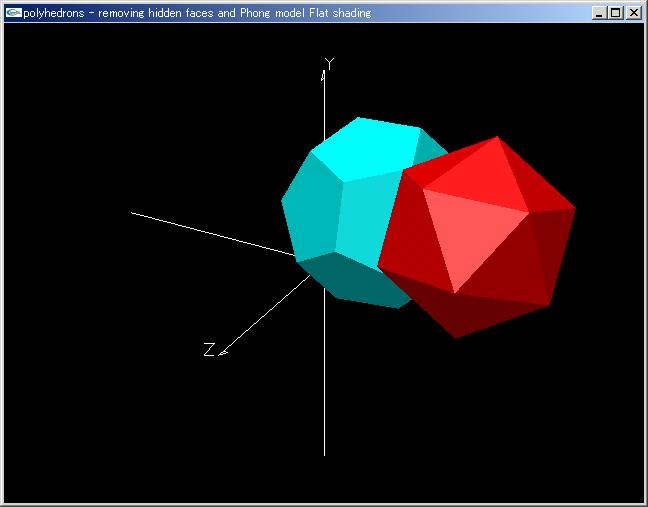二つの多面体表示アニメーションプログラム「polyhedrons.cpp」

課題　９
ファイル「drawtools3D.cpp」を用いて，正八面体表示アニメーションプログラム「octahedron.cpp」を作りなさい。正八面体は重心から6つの頂点までの距離が等しく，重心と各頂点を結ぶ線分は互いに直交するか，同一直線上になることを利用すると良い。
提出はWeb公開とし，ファイル名は「octahedron.txt」としなさい。また画像ファイルは「octahedron.gif」としなさい。

８．２　曲面で構成される立体の表現
球のような曲面で囲まれた立体は，擬似多面体で近似する。擬似多面体を構成した後，そのまま多面体として表示する方法をフラットシェーディング（flat shading）と呼ぶ。フラットシェーディング（図８．２）では，各面の法線ベクトルは，その面（三角形等の単純な多角形）の頂点の座標からその都度算出する。その面の色は，面の法線ベクトルを元にフォンモデルによる面の色の設定方法によって決定される。
これに対し，スムーズシェーディング（smooth shading）は，擬似多面体を曲面風に描く手法である。スムーズシェーディングには，次に述べる2つの手法が有名である。
（１）擬似多面体の各面を構成する頂点位置の法線ベクトルを別に計算しておき，この法線ベクトルを元に頂点の色を決定し，その面全体をグラデーションで塗りつぶすグーローシェーディング（Gouraud Shading）（図８．３）
（２）擬似多面体の各面を構成する頂点位置の法線ベクトルを別に計算しておき，面内の各点の法線ベクトルを補完法によって求め，この法線ベクトルを元に各点の色を決定し塗りつぶすフォンシェーディング（Phong Shading）（図８．４）

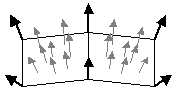図８．２　フラットシェーディング	図８．３　グーローシェーディング	図８．４　フォンシェーディング

球表示アニメーションプログラム「sphere.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。ここではグーローシェーディングが用いられている。

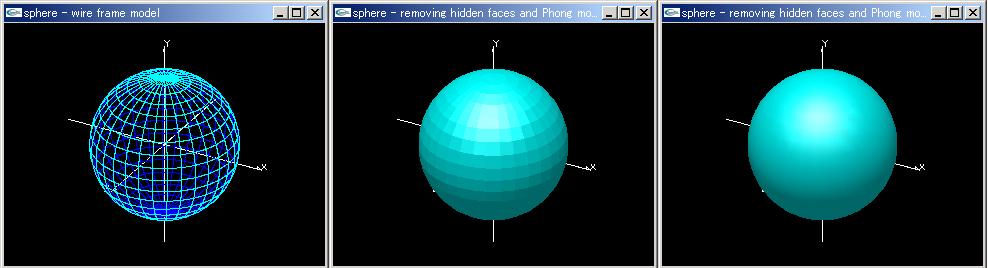
球表示アニメーションプログラム「sphere.cpp」 左：ワイアフレームモデル　中：フラットシェーディング　右：グーローシェーディング

球表示アニメーションプログラムの点の生成を表現したCGがあるので自分でコンパイルし実行しなさい。
このファイルは他のソースファイルを必要としないので単体でコンパイルすればよい。
球の点の生成表示アニメーションプログラム「HTMsphere.cpp」

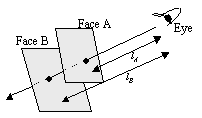
複数の面からなる立体を表示する時，各面の法線ベクトルを見ながら，その面を描くかどうか判断しながら描くだけでは，うまく描けないことがある。見 える面同士が重なっている場合，後方の面を描き，その後手前の面を描き，後の面に重ねて描けば自然な描写になる。このような手法はZソート法（図8.5参 照）と呼ばれる。Zソート法では，描くことになるすべての面を，その面の代表点のｚ座標で視点から遠い順にソートしておき，面を遠い順に描いてゆくと，手 前の面が遠方の面を覆って，自然な立体の表示が出来る。

図８．５　Zソート法

2つの面が前後に重なる場合でなく，２つの面が交差する場合はZソート法では解決できない。面を描く時，面の内部点1点1点を描く際に，その点のZ 座標を，画面を構成する点数と同じサイズのバッファに記憶して，別の点を重ね描きするかどうか検討する方法はZバッファ法と呼ばれている。
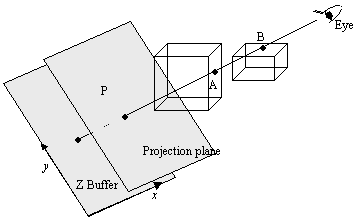
図8.6においてZバッファ法では，２つの面中の点A,点Bを描く際には，次のように描画している。
（１）点Aを先に描き，点Bを後から描く順の時
点Aを投影面に描き，点AのZ座標をZバッファ中に数値として記憶する。次に点Bを描こうとする時には点BのZ座標を現在のZバッファ値と比較して，点Bの方が手前にあることがわかるので投影面の点Aのところに点Bを重ね描きし，Zバッファに点BのZ座標を記憶する。
（２）点Bを先に描き，点Aを後から描く順の時
点Bを投影面に描き，点BのZ座標をZバッファ中に数値として記憶する。次に点Aを描こうとする時には点AのZ座標を現在のZバッファ値と比較して，点Bの方が手前にあることがわかるので点Aについての処理は中止する

図８．６　Zバッファ法

課題　10
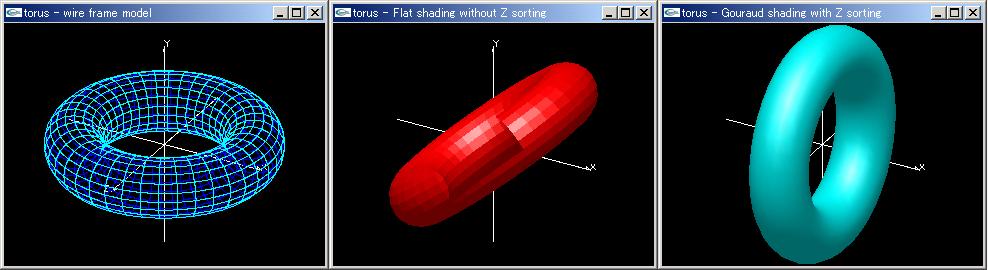
（１）環表示アニメーションプログラム「torus.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。赤い環表示の際に，環表示が不自然になる。また水色表示の際には環表示が自然になる。この差はどこから生じているか，プログラムを読んで考察しなさい。
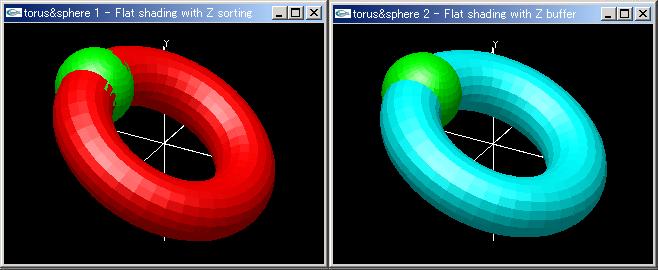
（２）球環表示アニメーションプログラム「torussphere1.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。赤い環表示の際に，球環接合部の表示が不自然になる。
球環表示アニメーションプログラム「torussphere2.cpp」を「drawtools3D.cpp」「drawtools3D.h」とともにコンパイルして実行しなさい。環表示が自然になる。この差はどこから生じているか，プログラムを読んで考察しなさい。
提出はWeb公開とし，ファイル名は「torussphere.txt」としなさい。

環表示アニメーションプログラム「torus.cpp」　左：ワイヤフレームモデル　中：面定義順描画　右：Zソート

球環表示アニメーションプログラム 「torussphere1.cpp」（左）Zソート法　　環と球のつなぎ目が不自然 「torussphere2.cpp」（右）Zバッファ法　描画が遅いが自然な描画

８．３　C++のクラスによる記述

多面体および曲面で構成される立体についてクラスで記述してみよう。物体の色および光の効果を与える物体の属性もこのクラス中に記述する。遠近感の 表現，光の効果の光源方向などは表示のクラスに記述する。また変換行列の設定は，頂点の座標と，法線ベクトルでは異なる演算なので，これらも表示のクラス に加えることとした。

立方体表示アニメーションプログラム「cubewithClass.cpp」を「CGCore3D.cpp」「CGCore3D.h」とともにコンパイルして実行し，プログラム各部の働きを検討しなさい。
立方体表示アニメーションプログラム「cubeDemowithClass.cpp」を「CGCore3D.cpp」「CGCore3D.h」とともにコンパイルして実行し，プログラム各部の働きを検討しなさい。
球表示アニメーションプログラム「spherewithclass.cpp」を「CGCore3D.cpp」「CGCore3D.h」とともにコンパイルして実行し，プログラム各部の働きを検討しなさい。
環表示アニメーションプログラム「toruswithclass.cpp」を「CGCore3D.cpp」「CGCore3D.h」とともにコンパイルし，プログラム各部の働きを検討しなさい。

課題　11
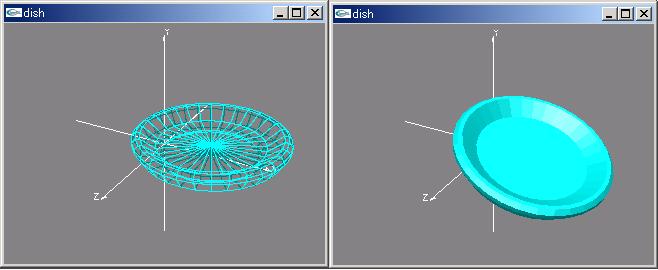
xy平面上の１１個の 点{0,0.15}，{0.7,0.15}，{0.9,0.3}，{0.95,0.3}，{1,0.25}，{1,0.2}，{0.9,0.05}， {0.7,0.05}，{0.65,0}，{0.6,0.05}，{0,0.05}を結んだ線をy軸を中心に回転させ，回転体を構成しこれを表示するプロ グラムを作りなさい。「drawtools3D.cpp」「drawtools3D.h」または「CGCore3D.cpp」「CGCore3D.h」を利用してよいが，利用しなくても良い。
いずれにしても，面の描き順の考慮（Zソート）は自分で行なうこと。
提出はWeb公開とし，ファイル名は「dish.txt」としなさい。また画像ファイルは「dish.gif」としなさい。

課題１１の実行例

９．　OpenGLのZバッファを用いた３次元図形の描画
前節までは，コンピュータグラフィックスの原理を学ぶために，OpenGLが備えているZバッファを用いた３次元図形の描画機能を用いなかった。この節ではOpenGLが提供しているCG環境を紹介する。
OpenGLは次のような機能をあらかじめ備えているため，ユーザがプログラミングする時，これらのことを自分で計算する必要がない。
（１）Zバッファを用いた面の交差，重なりの処理
（２）光の効果
（３）遠近感処理
（４）ティルティング
（５）フォンシェーディングによるスムーズシェーディング
（６）変換行列の生成と積の演算
OpenGLについての細かな説明は多くのWebサイトが見つかるので，各自検索すること。
次にいくつかのデモプログラムを示す。

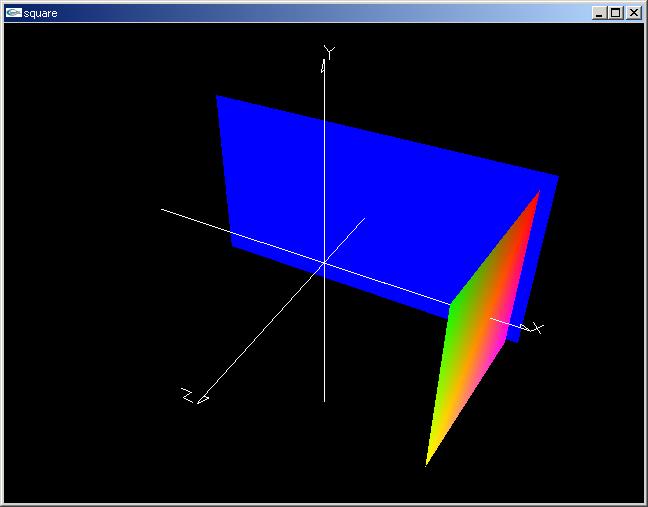
「GLsquare.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。Zバッファを用いた線，面の交差，重なりの処理が行なわれていることがわかる。このプログラムでは光の効果は使っていない。

プログラム「GLsquare.cpp」

「GLcube.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。変換行列の生成の仕方がわかる。変換行列の生成順は，後で行なう変換ほど先に記述する。これは，先に記述したものほど，数式上で，前になることに対応している。このプログラムでは光の効果は使っていない。

「GLcubewithlight.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。光の効果を導入している。

「GLpolyhedrons.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。

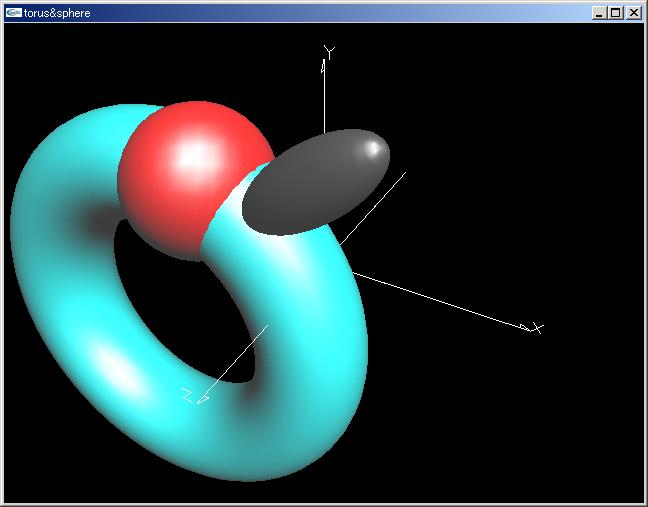
「GLtorussphere.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。このような図形もフォンシェーディングで高速に描画される。

プログラム「GLtorussphere.cpp」

「GLprovidedObjects.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。OpenGLが予め用意してある正多面体，球などは自分でデータを作らなくても良いことになっている。またデモとしてティーポットも用意されている。

「GLwithMouse1.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。このような図形も基本図形から生成される。またマウスの利用はすでに取り上げたものをそのまま使用している。

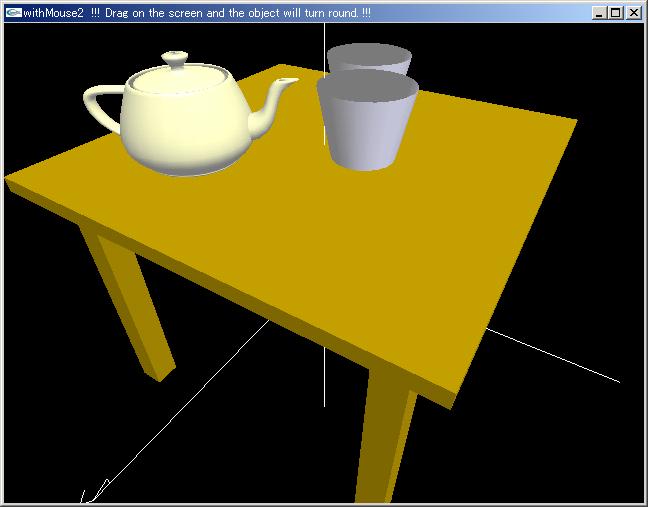
「GLwithMouse2.cpp」を「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイルし，実行しなさい。

プログラム「GLwithMouse2.cpp」

課題12
GlwithMouse1.cppをよく読むと，立方体４つでテーブルが作られているのがわかる。
GlwithMouse1.cpp をもとにして，情報工学科棟を３D表示し，マウスで視点を変えられるようにしなさい。どこまで正確に作るかは問わないことにしますが，できるだけ正確に作 りなさい。提出はWeb公開とし，ファイル名は「creativeCG.txt」としなさい。また画像ファイルは「creativeCG.gif」としな さい。

プログラム「JBuilding0.cpp」 （途中） 「GLDrawingtool3D.cpp」「GLDrawingtool3D.h」とともにコンパイル