2022.12.15 Coskx Lab　　

１　はじめに

小型DCブラシモータをモータドライバICでPWM駆動するとき，2つの駆動方式があります。
2つの駆動方式において，同じPWM周期，同じデューティ比で駆動したとき，モータの電流値がどうなるかを観察したいと思います。
PWM周期はmicro:bitのデフォルト周期である20msecを使用します。
pwm周期20msecは測定対象の電気的時定数に対して200倍の大きさです。
PWM周波数は50Hzとなりますが，これはDCモータのPWM駆動としては，かなり低い周波数です。

２　モータドライバICのふるまい

DCブラシモータ駆動にはモータドライバICが使われますが，その2つの入力信号と，モータ駆動電流の流れは次のようになっています。
IN1,IN2の信号とモータドライバの各FETの動作は次の表のようになります。

IN1	IN2	左上 FET	左下 FET	右上 FET	右下 FET	電流状態	モータの状態
High	Low	ON	OFF	OFF	ON	正転通電	正転
Low	High	OFF	ON	ON	OFF	逆転通電	逆転
Low	Low	OFF	OFF	OFF	OFF	絶縁	停止（フリー）
High	High	OFF	ON	OFF	ON	ショート	停止（ショートブレーキ）

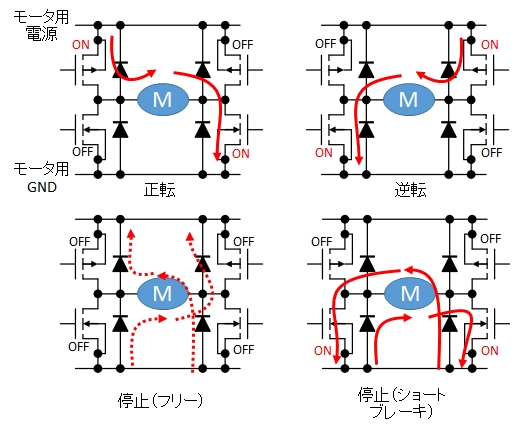
そして，各状態での電流の流れ方は次のようになります。
停止（フリー）のときは，ダイオードを経由して電源側に電流を流すことができます。
停止（ショートブレーキ）のときは，ダイオードの働きにより，モータの両端子がショートする状態になります。

３　2つのPWM駆動方式

モータドライバICで，モータを駆動するとき，高速にON-OFFを繰り返し，ONの時間とOFFの時間を調整する方法はPWM駆動と呼ばれます。
高速にON-OFFを繰り返す周期はPWM周期，1周期中のONになっている時間の割合はデューティ比と呼ばれます。
モータドライバICで，PWM駆動を実現するときには2つの駆動方式が考えられます。
PWM信号を使った2つの駆動方式とは次のようなものです。

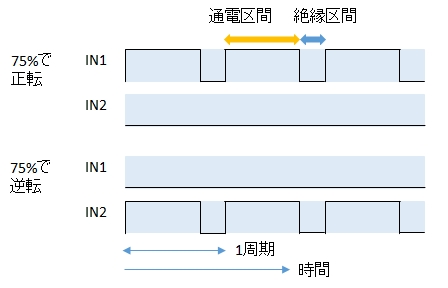
通電・絶縁駆動
例えば，デューティ比75%順方向駆動のとき，75%順方向駆動，25%停止（フリー）で動作させます。




通電・ショート駆動
同じように，デューティ比75%順方向駆動のとき，75%順方向駆動，25%停止（ショートブレーキ）で動作させます。




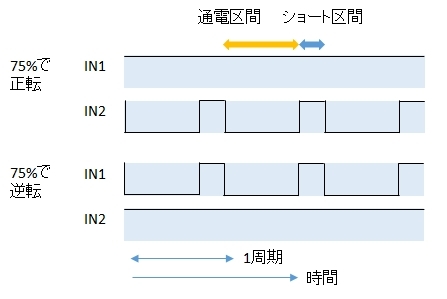
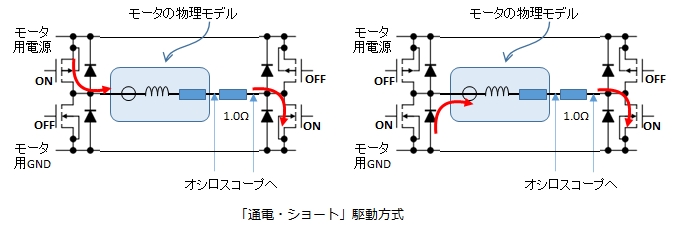
2つの駆動方式では，停止区間での電流の流れ方に違いがあります。

４　DCブラシモータについて

DCモータには，内部に巻き線があり，これはインダクタンス成分となります。またこの巻き線は線が細く長いため，抵抗があります。
また，モータが回転しているときは発電機として働き，逆起電力も働きます。逆起電力として発生する電圧は，モータの回転速度に比例しています。（モータが回転していないときには，発生する電圧は0Vです。）
すなわちDCモータはインダクタンス\(L\)と純抵抗\(R\)と電圧発生器」の直列結合とみなすことが出来ます。
インダクタンス\(L\)と純抵抗\(R\)を直接測定することは難しいですが，小型模型用130モータの純抵抗は1.5Ω程度(1.5Vでストール電流2.2Aより)とされています。

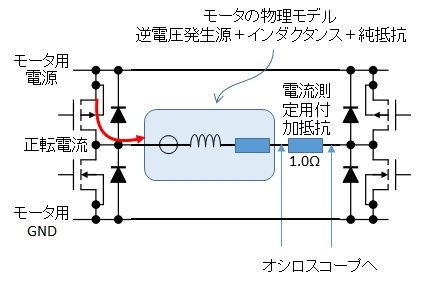
５　電流観察の方法

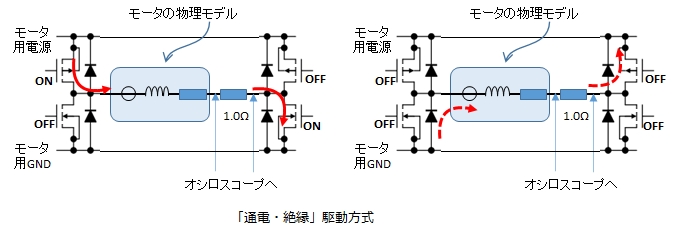
DCモータを流れる電流を直接測定することができないので，モータと直列に1.0Ωの抵抗を使い，その両端に生ずる電圧をオシロスコープで観察することにします。
測定時には見かけ上，モータの純抵抗が1.0Ω増えたことになります。

micro:bitとモータドライバのGNDは共通になっていますが，オシロスコープのGNDは電気的には浮いている状態で測定します。（この点は気を付けないと，意図しない回路ができてしまうので注意が必要です。）
モータの電源には定電圧電源を使用し，micro:bitの電源にはモバイルバッテリを使用してオシロスコープのGNDを共通化しないようにしました。
モータの電源電圧は4.5Vを使用しています。
モータドライバはTB6612FNG，DCモータは小型模型用130モータ（38.2減速ギヤ組み込み）を使用しています。

６　電流観察のために使用したmicro:bitのプログラム

micro:bitの端子のうち，PWM信号を発生することが出来，PWM周期，デューティ比を自由に生成できる端子は限られています。ここではP0，P1の2つの端子を使い，モータドライバのIN1,IN2の信号とします。

通電・絶縁駆動方式ではP0をL（0）に固定してP1に所望のデューティ比のPWM信号（正パルス）を発生します。アナログ値1023を与えたときにデューティ比は100%になります。
このプログラムでは，PWM周期20000μsecに設定し，アナログ値256を設定しているので,デューティ比25%での駆動になります。



通電・ショート駆動方式ではP0をH（1）に固定してP1に所望のデューティ比のPWM信号（負パルス）を発生します。与えたいパルス幅を1023から引いた値を設定します。
このプログラムでは，PWM周期20000μsecに設定し，アナログ値767(=1023-256)を設定しているので,デューティ比25%での駆動になります。

７　電流観察

PWM周期を20msecとし，2つの駆動方式でモータを駆動し，デューティ比を変化させて，電流観察します。
モータが回転すると。逆起電力が発生し，現象が複雑になるので，モータ軸を強制固定した時の測定も行います。

7.1　通電・絶縁駆動方式での電流観察

通電・絶縁駆動方式では，正転通電と絶縁をPWM周期で繰り返します。

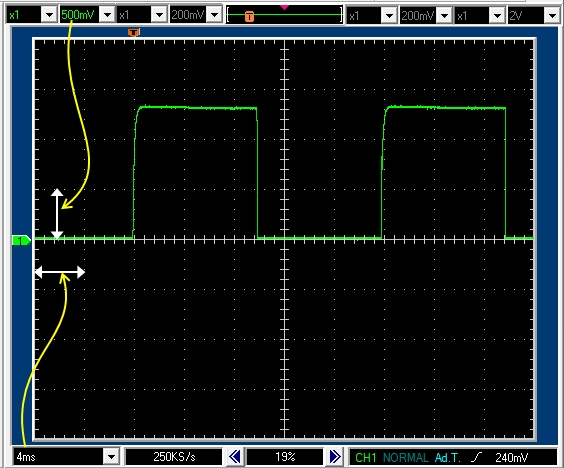
7.1.1 PWM周期 20msec デューティ比50% モータ軸を強制固定

モータ軸を強制固定しないと軸が回転し，逆起電力が発生します。出来るだけ純粋な状態を測定したいので，モータ軸を回転しないように強制固定しました。
PWM周期20msecデューティ比50%で10msecのパルスがあります。パルス高は1.4Vなので正転駆動区間では1.4Aの電流が流れていることがわかります。
パルスの立ち上がりでは，インダクタンスの作用で，電流の立ち上がりがややなまっているのがわかります。
パルスの立下りでは，絶縁状態になるのでなまりはありません。

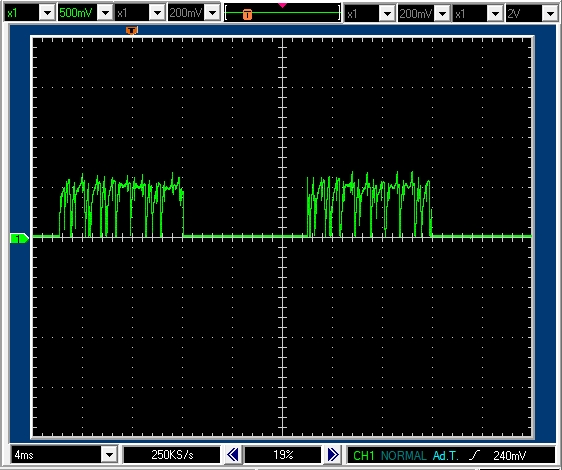
7.1.2 PWM周期 20msec デューティ比50% モータ軸は自由に回転

モータ軸が回転し，逆起電力が発生します。
PWM周期20msecデューティ比50%で10msecのパルスがあります。パルス高は0.5Vなので正転駆動区間では0.5Aの電流が流れていることがわかります。
発生している逆起電力は強制固定時の1.4Vとの差である0.9V程度となります。
（逆起電力による発生電圧は回転数に比例します。)
停止（フリー）区間では，当然ですが電流はOFFになっています。
なお，パルスのギザギザは，DCモータ回転中のブラシの切替の影響と思われます。

7.1.3 PWM周期 20msec デューティ比25% モータ軸を強制固定

PWM周期20msecデューティ比25%で5msecのパルスがあります。パルス高は1.4Vなので正転駆動区間では1.4Aの電流が流れていることがわかります。
パルスの立ち上がりでは，インダクタンスの作用で，電流の立ち上がりがややなまっているのがわかります。

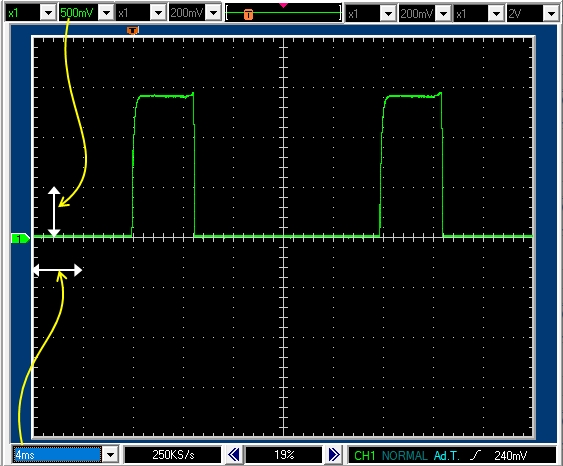
7.1.4 PWM周期 20msec デューティ比25% モータ軸は自由に回転

モータ軸が回転し，逆起電力が発生します。
PWM周期20msecデューティ比25%で5msecのパルスがあります。パルス高は0.7Vなので正転駆動区間では0.7Aの電流が流れていることがわかります。
発生している逆起電力は強制固定時の1.4Vとの差である0.7V程度となります。
停止（フリー）区間では，当然ですが電流はOFFになっています。
なお，パルスのギザギザは，DCモータ回転中のブラシの切替の影響と思われます。

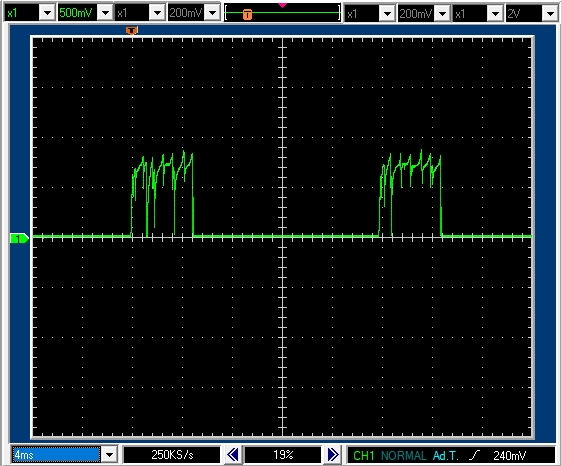
7.1.5 PWM周期 20msec デューティ比10% モータ軸を強制固定

PWM周期20msecデューティ比10%で2msecのパルスがあります。パルス高は1.3Vなので正転駆動区間では1.3Aの電流が流れていることがわかります。(他の測定で1.4Vだったので。0.1Vくらいの誤差はあると考えられます。）
パルスの立ち上がりでは，インダクタンスの作用で，電流の立ち上がりがややなまっているのがわかります。

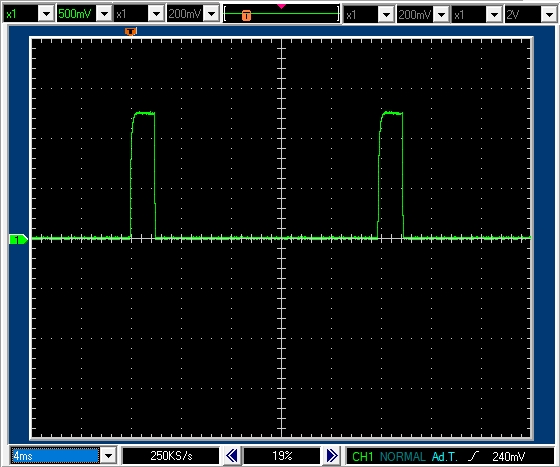
7.1.6 PWM周期 20msec デューティ比10% モータ軸は自由に回転(ゆっくり回転)

モータ軸は固定していませんが，回転を始めることができない状態です。
PWM周期20msecデューティ比10%で1msecのパルスがあります。パルス高は1.2Vなので正転駆動区間では1.2Aの電流が流れていることがわかります。
発生している逆起電力は強制固定時の1.3Vとの差である0.1V程度となります。

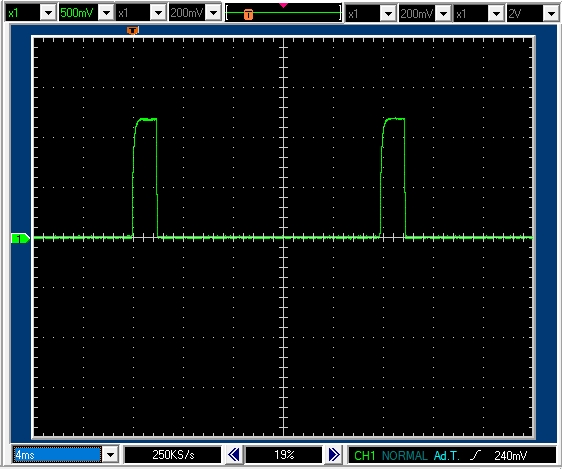
7.1.7 PWM周期 20msec デューティ比5% モータ軸は非固定ですが回転できず

モータ軸は固定していませんが，回転を始めることができない状態です。
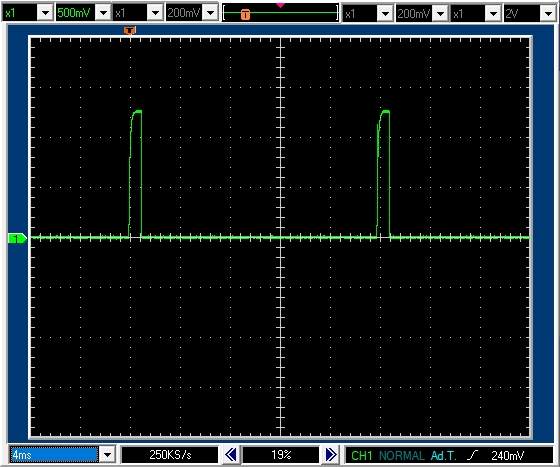
PWM周期20msecデューティ比5%で0.5msecのパルスがあります。パルス高は1.4Vなので正転駆動区間では1.4Aの電流が流れていることがわかります。
1周期の平均電流は，0.07Aとなり，この電流では，摩擦などの抵抗のため，モータ軸を回転させることが出来ません。

7.2　通電・ショート駆動方式での電流観察

通電・ショート駆動方式では，正転通電とショートをPWM周期で繰り返します。

7.2.1 PWM周期 20msec デューティ比50% モータ軸を強制固定

PWM周期20msecデューティ比50%で10msecのパルスがあります。パルス高は1.4Vなので正転駆動区間では1.4Aの電流が流れていることがわかります。 パルスの立ち上がりおよび立ち下りでは，インダクタンスの作用で，電流の立ち上がりおよび立ち下りがややなまっているのがわかります。
7.1.1と比較すると，こちらは立下りのなまりがあります。これはGNDを経由して電流がしばらくの間流れ残っている状態です。

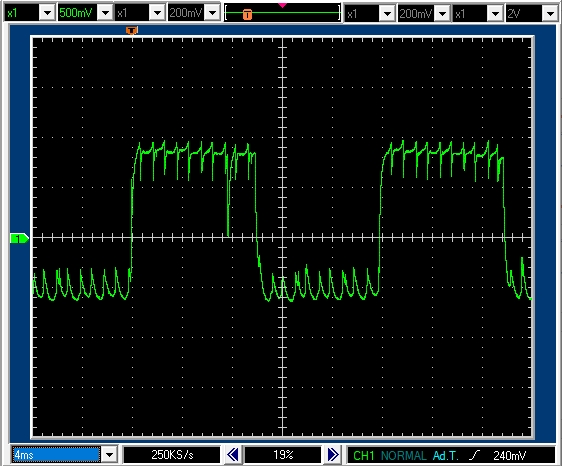
7.2.2 PWM周期 20msec デューティ比50% モータ軸は自由に回転

モータ軸が回転し，逆起電力が発生します。
PWM周期20msecデューティ比50%で10msecのパルスがあります。
パルス高は0.8Vなので正転駆動区間では0.8Aの電流が流れていることがわかります。
発生している逆起電力は強制固定時の1.4Vとの差である0.6V程度となります。
停止（ショートブレーキ）区間では-0.6Vなので，逆向きに0.6Aの電流が流れています。
この電流はGND経由で1周していて，抵抗で熱になります。
軸は回転しているので，逆起電力は常に0.6Vが発生していることになります。
なお，パルスのギザギザは，DCモータ回転中のブラシの切替の影響と思われます。
発生している逆起電力を見ても，ブラシの切替のギザギザ間隔を見ても，同じ50%のデューティ比駆動であっても，通電・絶縁駆動方式よりも回転数は低く，ゆっくり回っていることがわかります。

7.2.3 PWM周期 20msec デューティ比25% モータ軸を強制固定

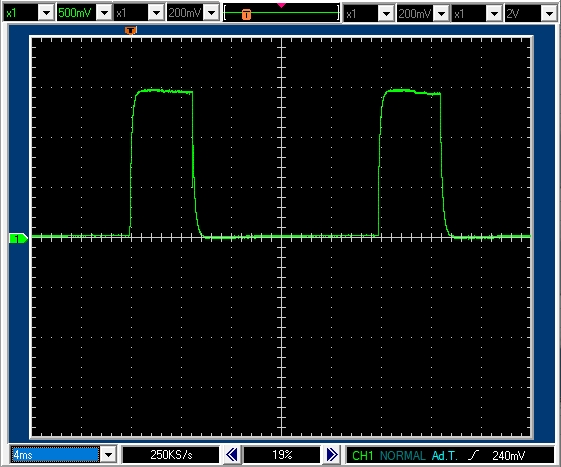
PWM周期20msecデューティ比25%で5msecのパルスがあります。パルス高は1.5Vなので正転駆動区間では1.5Aの電流が流れていることがわかります。「7.2.1」とは少し異なりますが，モータ軸の回転角が異なった位置で止まっているのでこれくらいは差が出ると考えられます。
パルスの立ち上がりおよび立ち下りでは，インダクタンスの作用で，電流の立ち上がりおよび立ち下りがややなまっているのがわかります。

7.2.4 PWM周期 20msec デューティ比25% モータ軸は自由に回転

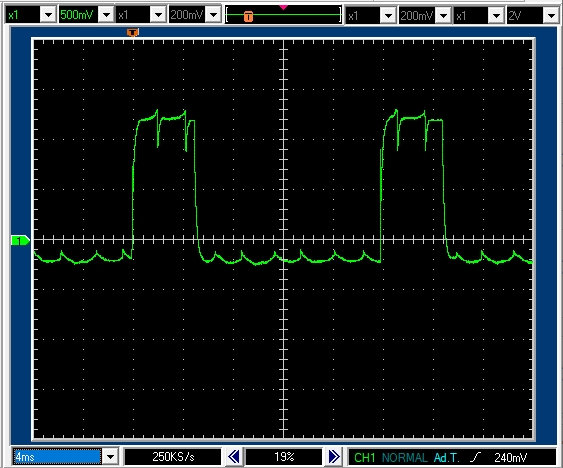
モータ軸が回転し，逆起電力が発生します。
PWM周期20msecデューティ比25%で5msecのパルスがあります。
パルス高は1.2Vなので正転駆動区間では1.2Aの電流が流れていることがわかります。
発生している逆起電力は強制固定時の1.5Vとの差である0.3V程度となります。
停止（ショートブレーキ）区間では-0.2Vなので，逆向きに0.2Aの電流が流れています。
この電流はGND経由で1周していて，抵抗で熱になります。
軸は回転しているので，逆起電力は常に0.3Vが発生していることになります。
なお，パルスのギザギザは，DCモータ回転中のブラシの切替の影響と思われます。
発生している逆起電力を見ても，ブラシの切替のギザギザ間隔を見ても，同じ25%のデューティ比駆動であっても，通電・絶縁駆動方式よりも回転数は低く，ゆっくり回っていることがわかります。

7.2.5 PWM周期 20msec デューティ比10% モータ軸を強制固定

PWM周期20msecデューティ比10%で2msecのパルスがあります。パルス高は1.3Vなので正転駆動区間では1.3Aの電流が流れていることがわかります。
パルスの立ち上がりおよび立ち下りでは，インダクタンスの作用で，電流の立ち上がりおよび立ち下りがややなまっているのがわかります。

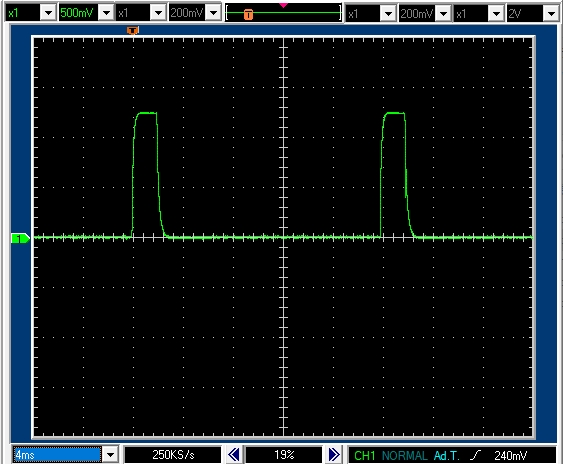
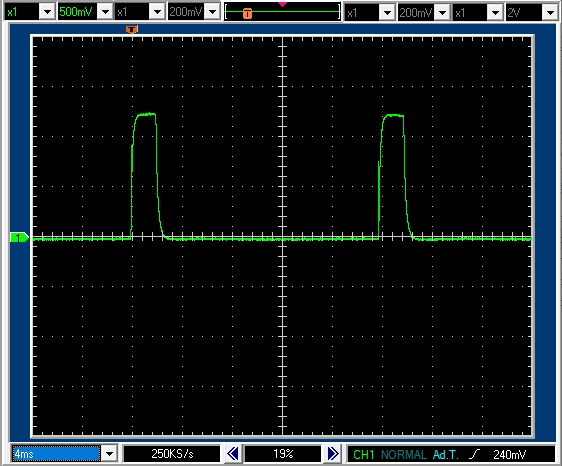
7.2.6 PWM周期 20msec デューティ比10% モータ軸は自由に回転(ゆっくり回転)

モータ軸が回転し，逆起電力が発生します。
PWM周期20msecデューティ比10%で2msecのパルスがあります。
パルス高は1.2Vなので正転駆動区間では1.2Aの電流が流れていることがわかります。
平均すると0.12Aが流れていることになります。
発生している逆起電力は強制固定時の1.3Vとの差である0.1V程度となります。
停止（ショートブレーキ）区間では-0.05Vなので，逆向きに0.05Aの電流が流れています。

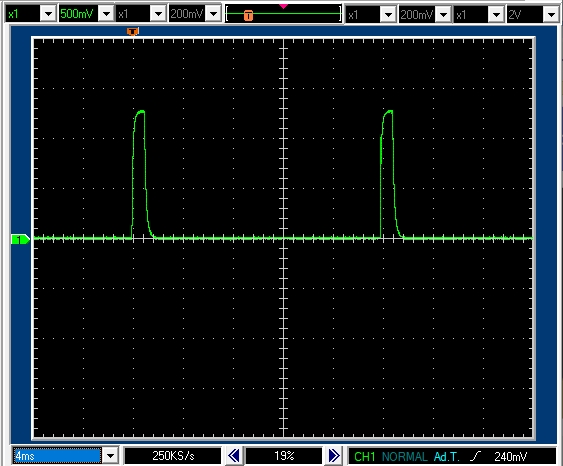
7.2.7 PWM周期 20msec デューティ比5% モータ軸は非固定ですが回転できず

モータ軸は固定していませんが，回転を始めることができない状態です。
PWM周期20msecデューティ比5%で1msecのパルスがあります。
パルス高は1.3Vなので正転駆動区間では1.3Aの電流が流れていることがわかります。
1周期の平均電流は，0.065Aとなり，この電流では，摩擦などの抵抗のため，モータ軸を回転させることが出来ません。

８　まとめ

2つのPWM駆動方式でDCモータを駆動したときの，モータを流れる電流の様子を観察しました。
PWM周期はmicro:bitデフォルトの20msecを使用しています。
このPWM周期は，ここで測定しているDCモータ回路の時定数 \(T = 100 \mu sec\) に対して \(200T\) になります。（補足参照）
ただし，モータと直列に1.0Ωを付けているため，見かけ上モータの純抵抗が1.0Ω増加したと考えての電流値になります。
通電・絶縁駆動では停止（フリー）区間では電流が流れないのに対して，通電・ショート駆動では，GNDを通して電流が流れるため，停止（フリー）区間で逆起電力方向に電流が流れます。
通電・絶縁駆動の方が，同じデューティ比（50%または25%のとき）では高速に回転します。通電・ショート駆動では，毎周期にショートブレーキを掛けているので，想定の範囲と思います。
なお低いデューティ比でのモータ動作においては，2つの駆動方式間に差異は見られません。（これはPWM周波数(50Hz)が極端に低いからです。1kHz以上のPWM周波数では差異が見られます。）

９　発展

DCモータ駆動に置けるPWM周期20ｍsecは大きすぎです。
小型DCモータではPWM周期1msecくらいが，よく使用されていると思います。
小さなPWM周期での電流観察も行いました。

PWM周期 4msec	≫
PWM周期 1msec	≫
PWM周期 0.4msec	≫

小さなPWM周期では，低デューティ比駆動の時モータ停止状態からの起動が困難（トルク不足になる）と言われていますが，これは「通電・絶縁駆動方式」のときに起こっていることがわかります。
「通電・ショート駆動方式」であれば，小さなPWM周期，低デューティ比駆動でもトルク低下がそれほど極端ではなくなっている様子がわかると思います。

補足　モータの電気的時定数

一般にインダクタンス \(L\) と抵抗 \(R\) の回路の両端にいきなり一定電圧を加えた時，回路の電流 \(i\) は，\(i(t)=K(1-\exp(-\frac{1}{T}t))\) で表されることが知られています。



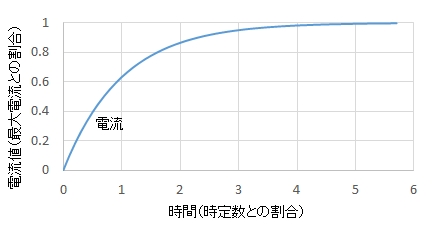
ただし，\(K\)はゲイン定数，\(T\)は時定数，\(t\)は時間です。
モータには電気的時定数と機械的時定数がありますが，ここでは電気的時定数です。
電気的時定数\(T\)は，\(T=L/R\) になります。 また，電気的時定数\(T\)は，パルスが立ち上がってから，パルス高の63%を通過するまでの時間に一致することも知られています。

電源電圧 \(E=4.5V\)，PWM周期 20msec デューティ比50% モータ軸を強制固定の測定（7.1.1参照）の時間軸を拡大すると，下図のオシロスコープ画像のようにパルスの立ち上がりの様子がよく見えます。
測定対象の合成抵抗 \(R_c\) を（モータドライバのFETのON時抵抗 \(R_d\) ＋モータの純抵抗 \(R_m\) ＋測定用抵抗 \(R_a(1.0\,\mathrm{\Omega})\)）とします。 下図のオシロスコープ画像から測定すると，合成抵抗 \(R_c\) ＋インダクタンス \(L\) の系の電気的時定数は，だいたい \(T = 100 \,\mathrm{\mu s}\) となりました。
また，この時の電流最大値は \(i_{max}=1.4A\) なので，測定対象の合成抵抗 \(R_c\) は \(R_c=E/i_{max}=4.5/1.4＝3.2\,\mathrm{\Omega}\) となっています。----（A)

ここで，モータドライバのFETのON時抵抗 \(R_d\) を推定します。
DCモータ取り外し，別な1.0\(\,\mathrm{\Omega}\)抵抗と差し替えて，電流を測定すると1.4Aとなりました。
4.5Vを加えているので，合成抵抗（モータドライバのFETのON時抵抗＋モータの代わりの\(1.0\,\mathrm{\Omega}\)抵抗＋測定用\(1.0\,\mathrm{\Omega}\)抵抗）は \(4.5/1.4＝3.2\,\mathrm{\Omega}\)となり，(モータドライバのFETのON時抵抗)は \(R_d=3.2-1.0-1.0=1.2\,\mathrm{\Omega}\)と推定されます。----（B)

（A)(B)よりモータの純抵抗 \(R_m\) は，\(R_m=R_c-R_d-R_a=3.2-1.2-1.0=1.0 \,\mathrm{\Omega}\) と推定されます。

インダクタンス \(L\) と抵抗 \(R_c\) の直列系の電気的時定数 \(T\) は，\(T = L/R_c \) で，合成抵抗が \(R_c=3.2 \,\mathrm{\Omega}\) でしたので，モータのインダクタンスはだいたい \(L = T \times R_c = 100 \times 3.2 = 320\,\mathrm{\mu H}\) と推定されます。
モータの純抵抗は \(R_m=1.0 \,\mathrm{\Omega}\) でしたので，モータ単体の電気的時定数は \(L/R_m = 320/1.0=320 \,\mathrm{\mu s}\) と計算上なります。

また，測定用抵抗が無ければ，合成抵抗はモータドライバのFETのON時抵抗＋モータの純抵抗＝\(1.2＋1.0＝2.2\,\mathrm{\Omega}\)のみなので， モータドライバとDCモータだけの電気的時定数は，\(L/R = 320/2.2=150 \,\mathrm{\mu s}\) と推定されます。

モータ(合成抵抗＋インダクタンス)の電気的時定数の測定のモデル 合成抵抗＝ドライバFETのON抵抗＋モータの純抵抗＋測定用1Ω抵抗

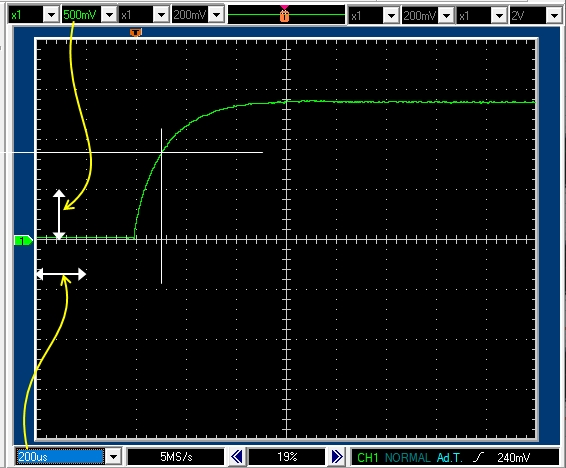
モータ軸強制固定時のモータ(合成抵抗＋インダクタンス)の電気的時定数の測定結果 縦軸の電圧は測定用1Ω抵抗の両端電圧なので，1Vは電流1Aに相当する