見慣れた座標系と同じになるように,右側を+方向とします。速度も右方向に走行する場合が+方向となります。
またモータ指令値も右方向に進める場合が+方向となります。
カートの現在位置を\(x\),目標位置を\(r\)とします。
次の場合はカートを右側に進めたいので,モータ指令値は正の値になります。
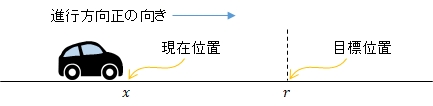
次の場合はカートを左側に進めたいので,モータ指令値は負の値になります。

なお座標原点はどこにあってもよいことになります。
2021.9.25 Coskx Lab
1 座標のとり方
プログラムにまで仕上げることを考えると座標をどうとるかは重要です。
見慣れた座標系と同じになるように,右側を+方向とします。速度も右方向に走行する場合が+方向となります。
またモータ指令値も右方向に進める場合が+方向となります。
カートの現在位置を\(x\),目標位置を\(r\)とします。
次の場合はカートを右側に進めたいので,モータ指令値は正の値になります。

次の場合はカートを左側に進めたいので,モータ指令値は負の値になります。

なお座標原点はどこにあってもよいことになります。
2 制御則
「カートの現在位置から,モータ指令値を決めるルール」のことを制御則と言います。
リモコンを使って,走行中のカートの動きを見ながら停止線で止める操作は,上手下手の違いはありますが,子供でもちょっと練習すればできるようになります。
うまく停止線で止めるにはコツが必要ですが,そのコツを修得しても,うまく言葉で言い表せない場合が多いです。
コツをうまく言葉で表し,図示したり数式で表せたりするとそれが制御則になります。
制御則は単純なものから複雑なものまであります。
単純な考え方から,順にいろいろな考え方を取り上げて,それを制御則にしてみます。
3 目標位置でモータOFFする (素朴なアイディア)
アイディアの明確化
「スタートから,目標位置まで全力で進み,目標位置を通り過ぎたらモータ指令値を0にする」という制御則を考えます。
この制御則では誰が考えても失敗します。
どこで止まるかはカートに聞いてくれ状態になり,目標位置を必ず行き過ぎてから止まります。
スタート時に\(x<r\) のときは全力前進なのでモータ指令値は正ですが,スタート時に\(r<x\) のときは全力後退なのでモータ指令値は負になります。
このアイディアを図示すると次の図のようになるでしょう。
この図は,ある時刻にモータ指令値をどうするかを示しているのではなく,カートがどこにいたらどのようなモータ指令値を与えるかということを示しています。
(「モータ指令値\(y\)」を「カートの現在位置\(x\)」の関数として表していることになります。)
(A)スタート時に\(x<r\) のとき
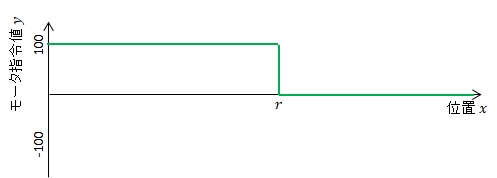
(B)スタート時に\(r<x\) のとき
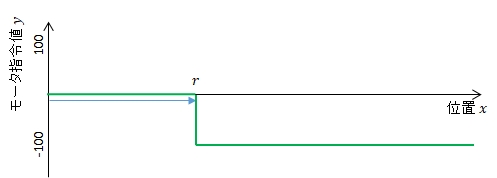
現在位置\(x\),モータ指令値\(y\)として,制御則を式で表現すると次のようになるでしょう。モータ指令値の範囲は-100から+100としています。
(A)スタート時に\(x<r\) (停止目標位置が右にある)のときの制御
$$y=\left \{ \begin{array}{cr}
100 & (x<r) \\
0 & (r\leqq x) \\
\end{array}\right.$$
(B)スタート時に\(r<x\) (停止目標位置が左にある)のときの制御
$$y=\left \{ \begin{array}{cr}
0 & (x<r) \\
-100 & (r\leqq x) \\
\end{array}\right.$$
人がこの制御則でカートを制御するときは,目視で,停止線を越えたかどうかを確認し,停止線を越えるまではモータ指令値最大でモータを駆動し,停止線を越えたらモータ指令値を0にするという(操作制御則)になります。
この制御則を使って,距離センサとモータを持つマイコンシステムにおいて制御プログラムを作成すると次のようになるでしょう。(\(x<r\) のときを考えます。)
無限ループしなさい
{
・距離センサから現在位置情報\(x\) を受け取る
・\(x<r\) ならば モータ指令値\(y\) を0にする
そうでないならば モータ指令値\(y\) を-100にする
・モータ指令値\(y\) でモータ駆動指令を出す
}
そうすると電源が切れるまで,この動作を続けます。カートの方は,惰性で目標位置を過ぎてもそのまま進んでしまいますが,摩擦抵抗などの影響で目標位置の先で停止するでしょう。
micro:bitで制御されたカートでの実験
走行フィールドの座標は次のようになっています。
モータ指令値の正の値は前進方向,負の値は後退方向の指令値を表します。
カートの現在位置も目標位置も負の値です。
座標原点に壁があります。
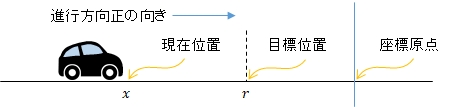
カートの実験ではモータ指令値を-60から+60の範囲に制限しています。
「目標位置でモータOFFする」制御則でカートを走行させ,実際の動作を確かめた結果を示します。カートの位置は,正面の壁までの距離をレーザ距離センサで測距して得ています。モータ指令値を60または0で駆動しています。
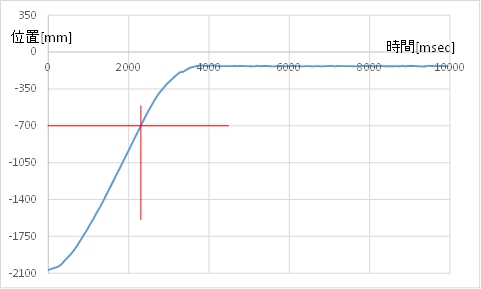
-2100mm付近でスタートし,モータ指令値60で走行します。-700mmでモータ指令値を0にするのですが600mmほど行き過ぎて-100mm位置くらいに停止します。
測定結果を実験グラフに示します。
(A)のグラフで,カート位置が-700になった時刻に,(B)のグラフで,モータ指令値が60から0になることがわかります。
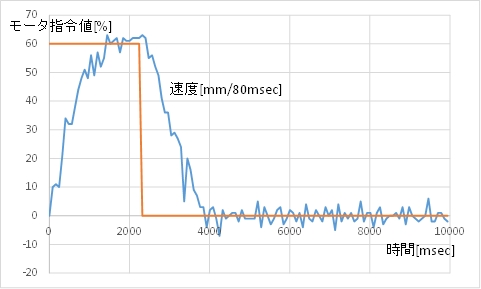
(B)のグラフのカートで,速度は起動直後大きくなり,モータ指令値が0になったのちに速度が低下している様子がわかります。その後,-100mm程度のところに停止しています。
ここで速度と言っているのは80m秒間に進んだ距離[mm]のことです。
(A) カート位置のグラフ
(B) モータ指令値(茶)とカートの速度(青)
次の動画は,-500mmでショートブレーキをかけて,止まるまでの距離を短くしたものです。
それにしても行き過ぎてから止まることには変わりありません。
4 行き過ぎたら戻る (素朴なアイディア)
アイディアの明確化
「3 目標位置でモータOFFする」の考え方では,行き過ぎてしまいます。行き過ぎたら戻ればよいので次のように考えます。
「目標位置手前なら全力前進,目標位置を越えたら全力後退にする」
この考え方を現在位置\(x\),モータ指令値\(y\)として図示すると次の図のようになるでしょう。
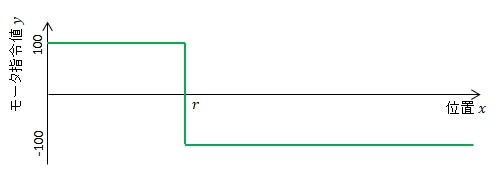
目標位置に左側から近づくことにすると,この制御則では,目標位置に到達し目標位置の右側に入ると左に全力で進めを指令します。左向きに力を受けている状態で速度を落としながら右に進んだ後,止まってしまい,すぐに左に動き始めます。再び目標位置の左側に入ると,右に全力で進めを指令します。右向きに力を受けている状態で速度を落としながら左に進んだ後,止まってしまい,すぐに右に動き始めます。また目標位置の右側に入ると,左に全力で進めを指令します。・・・というのを繰り返すことになります。
このように目標位置を中心に往復を繰り返してしまう振動が起こってしまい,なかなか止まらなさそうです。摩擦があるのでやがては止まるかもしれません。また,モータにしてみれば,全力前進と全力後退を交互に続けているので,かなり過酷な使われ方です。
目標停止位置に左から近づく場合でも右から近づく場合でも同じ制御則で対応できることになります。
現在位置\(x\),モータ指令値\(y\)として,制御則を式で表現すると次のようになるでしょう。モータ指令値の範囲は-100から+100としています。
$$y=\left \{ \begin{array}{cr}
100 & (x<r) \\
-100 & (r\leqq x) \\
\end{array}\right.$$
この制御ではモータ指令値が2つだけです。そのため2値制御と呼ばれます,ON-OFF制御も2値制御の一種です。
micro:bitで制御されたカートでの実験
走行フィールドの座標は次のようになっています。
座標原点に壁があります。

実験ではモータ指令値を-60から+60の範囲に制限しています。
この制御則でカートを走行させた様子をグラフに示します。
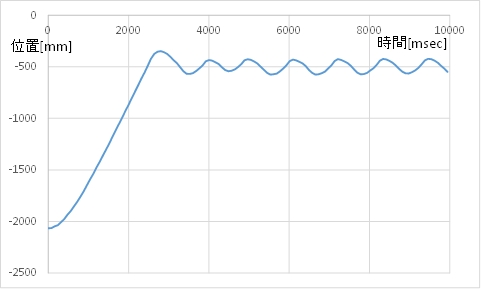
目標停止位置(-500mm)の前後で,モータ指令値が-60と60で交互に切り替わり,カートが前後に振動していることがわかります。振動し続けて止まりそうもありません。
(B)のグラフでは,正の速度を持っているときに,モータ指令値が負になっているところがあります。このとき,モータは正転しているのに,電流は逆転する方向に流れていて,強いブレーキ作用になります。
(A) カート位置のグラフ
(B) モータ指令値(茶)とカートの速度(青)
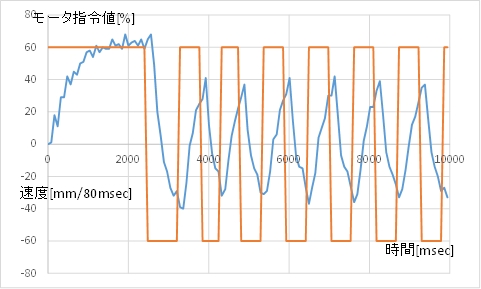
次の動画は,この制御則での制御です。なかなか止まりそうにありません。
グラフデータ採取と動画撮影は異なる走行です。
5 ここまでのまとめ
ここで取り上げた2つの制御則は,うまくいきそうもないことは予想できると思います。
制御則が単純で表現が簡単なので,導入部として取り上げました。
次はもう少しうまくゆく制御則を考えます。
リンク
| (0)表紙ページ フィードバック制御はじめの一歩 | ≫ |
| (1)ある位置に到達したらモータを止める(このページ) | ≫ |
| (2)目標位置前なら前進,行き過ぎたら後退 | ≫ |
| (比例制御) (3)目標までの距離に比例したモータ指令値を作る |
≫ |
| (比例微分制御) (4)目標までの距離と速度からモータ指令値を作る |
≫ |