2021.9.25 Coskx Lab　　

１　モータ指令値\(y\)を現在位置\(x\)の一次関数で表す

アイディアの明確化
多段の階段制御（N値制御）をみていると，モータ指令値の段数をもっと増やしたくなります。しかし場合分けがだんだん面倒になってきます。
（9値制御，指令値は25刻み　再掲）

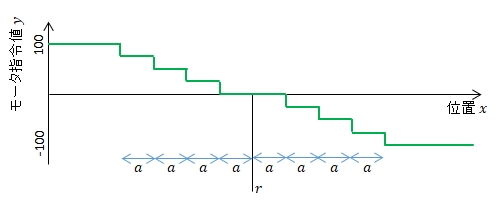
「目標位置周辺ではモータ指令値を一次関数で表す」方が簡単になりそうです。
この考え方を現在位置\(x\)，モータ指令値\(y\)として図示すると次のようになるでしょう。


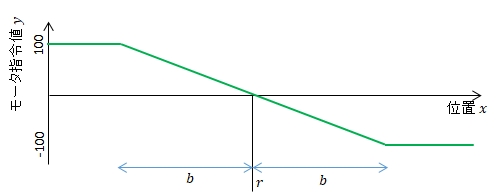
現在位置\(x\)，モータ指令値\(y\)として，制御則を式で表現すると次のようになるでしょう。モータ指令値の範囲は-100から+100としています。
$$y=\left \{ \begin{array}{cr} 100 & (x<r-b) \\ -\dfrac{100}{b}(x-r) & (r-b\leqq x<r+b) \\ -100 & (r+b\leqq x) \\ \end{array}\right.$$ \(b\)の値をどれくらいにするかは，実験で決めていきます。
（都合の良い値は見つからないかもしれません。）
\(y\)が\((x-r)\)に比例しているところは，比例制御と呼ばれます。比例制御は英語ではProportional Controlなので，P制御とも呼ばれます。
比例制御はフィードバック制御の基本的な制御です。

２　比例制御

「１」で比例制御を紹介しました。 比例制御の制御則を次のような表現に変更します。
$$y=\left \{ \begin{array}{cr} 100 & (x<r-b) \\ -k_p(x-r) & (r-b\leqq x<r+b) \\ -100 & (r+b\leqq x) \\ \end{array}\right.$$ \(k_p=\frac{100}{b}\)は比例定数でフィードバック係数あるいはフィードバックゲインと呼ばれます。
ここで
\(y_{tmp}=-k_p(x-r)\)とすると，\(y_{tmp}\)は次の図の点線になります。
\(y_{tmp}\)をそのままモータ指令値として与えると，モータには絶対値100以上の値が与えられてしまう場合が生じます。


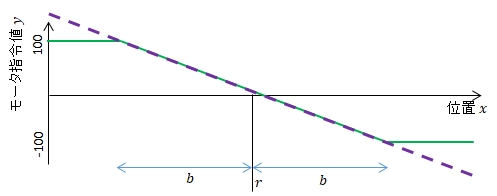
そこで\(y_{tmp}\)の絶対値が100を超えたところを100までに抑え込んでモータ指令値\(y\)とします。
$$y=\left \{ \begin{array}{cr} -100 & (y_{tmp}<-100) \\ y_{tmp} & (-100\leqq y_{tmp}<100) \\ 100 & (100\leqq y_{tmp}) \\ \end{array}\right.$$ この形の制御則では，フィードバック係数\(k_p\)を定めるだけで，切り替え点の値\(b\)を求める必要がなくなることから実用的です。
フィードバック係数\(k_p\)が小さな場合には，目標位置のかなり手前から減速を始めてしまいます。
フィードバック係数\(k_p\)が大きな場合には，（極端な場合は2値制御と同じになってしまいます）目標位置で往復を繰り返す振動が残ってしまい，良くない制御になってしまいます。しかし多少振動が残る位の方が目標位置に速く到達します。

micro:bitで制御されたカートでの実験
比例制御では，フィードバック係数\(k_p\)によって，カートの走行の様子が変化します。 そのため，フィードバック係数\(k_p\)を0.1，0.2，0.4，0.8，1.6と変化させて，実験しています。目標位置\(r\)は-500mmです。
フィードバック係数\(k_p\)が小さな時ほど，早く（目標停止位置から離れたところから）減速を始めるのがわかると思います。
またフィードバック係数\(k_p\)を大きくすると，減速を始めるのが遅くなり（高速で走行している時間が長い）目標位置に到達するのは早くなり，より強く目標停止位置に近づこうとしますが，振動も激しくなります。
また，モータ指令値の絶対値が10程度以下になると，指令値は出ているのだけれど，モータの特性や摩擦などの影響でモータが回れないということが起こり，止まってしまいます。目標停止位置から離れたところに止まってしまうことがあります。また目標位置に近いところに停止するとしても，停止位置の再現性はそれほど高いわけではありません。（ここが現実の複雑なところです。）

ここで使用しているフィードバック係数\(k_p\)は（現在位置－目標位置）の単位をmmにしているときのものです。もし（現在位置－目標位置）の単位をcmにした場合には異なる値(10倍の値)になります。

(1)フィードバック係数\(k_p=0.1\) のとき
(A) カート位置のグラフ

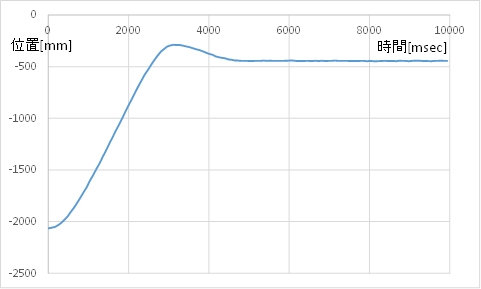
(B) モータ指令値（茶）とカートの速度（青）

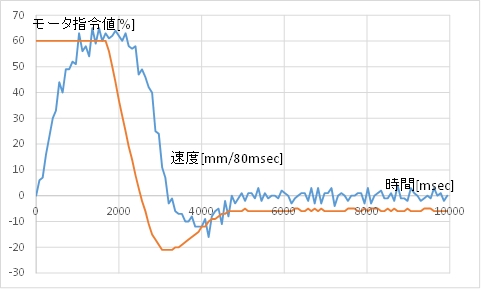
(C) 動画例　早くから負の指令値により減速しています。目標位置行き過ぎ後も戻る力が弱いです。


(2)フィードバック係数\(k_p=0.2\) のとき
(A) カート位置のグラフ

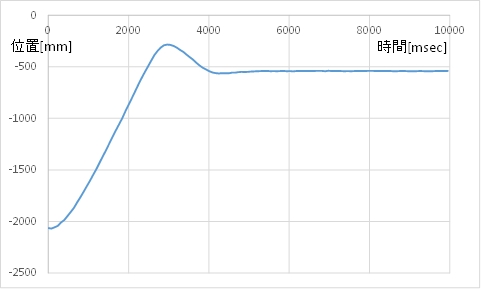
(B) モータ指令値（茶）とカートの速度（青）

(C) 動画例　まだ目標値に吸い寄せられる感じはしません。


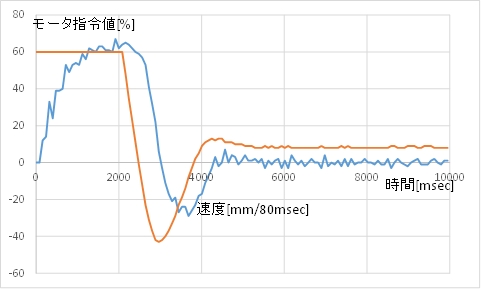
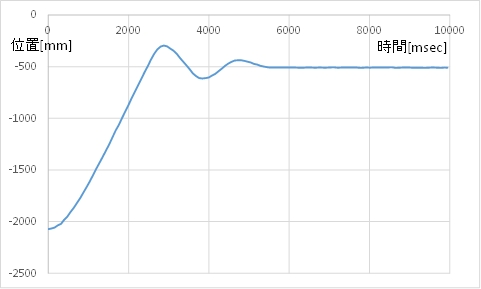
(3)フィードバック係数\(k_p=0.4\) のとき
(A) カート位置のグラフ

(B) モータ指令値（茶）とカートの速度（青）

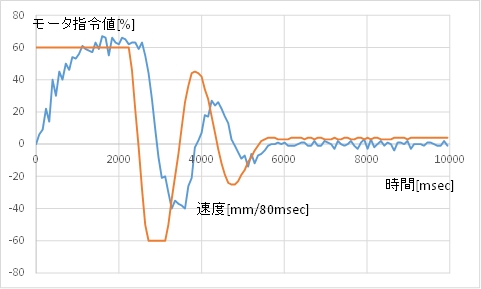
(C) 動画例　目標値に吸い寄せられる感じが出てきました。


(4)フィードバック係数\(k_p=0.8\) のとき
(A) カート位置のグラフ

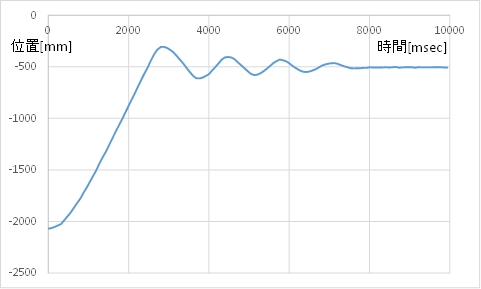
(B) モータ指令値（茶）とカートの速度（青）

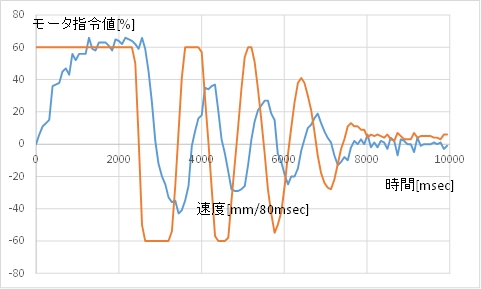
(C) 動画例　目標値に吸い寄せられる感じがしますが，目標位置前後の振動の減衰が遅いです。


(5)フィードバック係数\(k_p=1.6\) のとき
(A) カート位置のグラフ

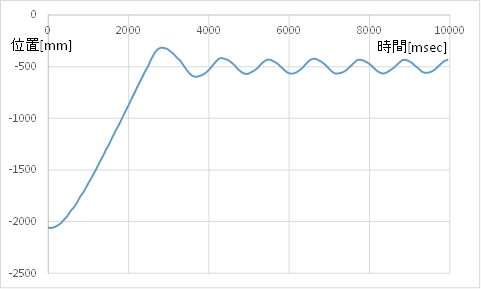
(B) モータ指令値（茶）とカートの速度（青）

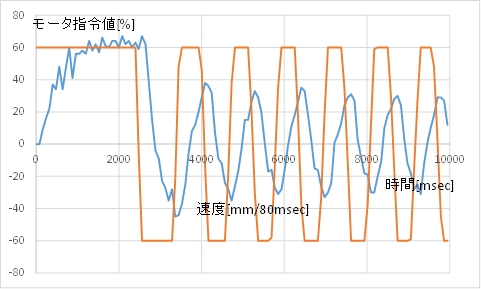
(C) 動画例　目標位置前後の振動がなくなりません。

３　フィードバック係数の意味

カートを目標位置に置いて，制御を続けたとします。
目標位置にいるので，モータへの指令値は0です。
もし，\(k_p=1.0\)とすると，　\(y=k_p\times 位置のずれ\)　なので，カートが目標位置から100mmずれたところにいるとモータ指令値は100(全力走行)になります。ここでの実験では，モータ指令値の絶対値を60に制限しているので，カートが目標位置から60mmずれたところにいるとモータ指令値は60(全力走行)になります。
もし，\(k_p=0.1\)とすると，カートが目標位置から1000mmずれたところにいるとモータ指令値は100(全力走行)になります。ここでの実験では，モータ指令値の絶対値を60に制限しているので，カートが目標位置から600mmずれたところにいるとモータ指令値は60(全力走行)になります。
この感覚がフィードバック係数です。

カートを目標位置に置いて，制御を続けているとします。
手でカートの位置をずらしてみると，ずれの値に比例する戻ろうとする力を感じます。この体験は，ばねを手で伸ばしたり縮めたりするときの感覚に似ています。フィードバック制御は見えないばねでカートを目標位置に押し戻そうとするのと同じであることがわかると思います。

４　ここまでのまとめ

階段制御（他値制御）を十分細かく行うと，比例制御に行きつくことがわかったと思います。
比例制御ではフィードバック係数が重要で，係数値が小さすぎると，目標位置に吸いつくような動作ができません。また係数値が大きすぎても振動が止まらなくなって，困った状態になります。
程よいフィードバック係数を選んでも，振動が起こってしまう欠点も見えました。
大きなフィードバック係数を使って，目標位置に吸いつくような動作を引き出し，しかも 振動を起こさないようにできれば良い制御になります。
もうひとひねり工夫が必要です。

リンク

(0)表紙ページ　フィードバック制御はじめの一歩	≫
(1)ある位置に到達したらモータを止める	≫
(2)目標位置前なら前進，行き過ぎたら後退	≫
（比例制御） (3)目標までの距離に比例したモータ指令値を作る（このページ）	≫
（比例微分制御） (4)目標までの距離と速度からモータ指令値を作る	≫