2021.9.25 Coskx Lab　　

１　振り子の振動をはやく減衰させるにはどうしたらよいか

比例制御において，目標位置で往復を繰り返してしまい，その振動がなかなか減衰しない場合の対策を考えます。
よくできた振り子はなかなか振動が止まらないものです。例えば30cmの棒の先に1kgくらいのおもりを付け，うまく支えたら振動はなかなか減衰しないでしょう。
この振り子の振動を早く減衰させることを考えます。図のように振り子に大きな「風船」を付けたらどうでしょう。


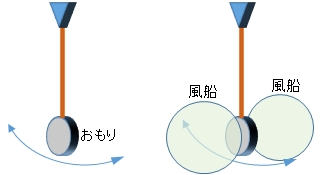
風船は，振り子のおもりに比べると，空気の抵抗を受けやすく，振動を減衰させる効果が期待できます。この図よりもっと大きな風船を付けると更に振動の減衰ははやくなります。
おもりだけの振り子でも水中で振動させたらもっと急速に振動振幅は小さくなります。 どろどろの重油の中では，振り子は往復運動もできずにずるずると動いて時間をかけて最下点で止まるという運動になるかもしれません。

風船や水の役割は何かというと，運動に対する止めようとする抵抗（粘性抵抗）です。
空気や水の抵抗は複雑ですが，近似的に速度の3乗に比例して大きくなるといわれています。人間もプールの中で立ち止まっているときは，前にも後ろにも押されませんが，プールの中を前に向かって歩き始めると後ろに向かって押されます。（前に進みにくくなります。）「速度に応じた，止めようとする力」が働いていることになります。
振り子も最下点周辺では速度を持ち，風船などを用いれば「速度に応じた，止めようとする力」が働くので振動が早く収まるようになります。

２　カートの振動をはやく減衰させる

振り子と同じことを風船などを使わずにカートで起こせばよいことになります。速度の3乗に比例していなくても，速度に比例するくらいの止めようとする力を生じさせればよいでしょう。すなわち次の図のような速度に比例する逆向きの力がカートに働けばこの考え方が達成できます。



速度\(v\)に比例する逆向きの力\(f\)は数式でいうと
$$f=-k_v v$$ になります。（\(k_v\) は比例定数）
どうしたら，速度に比例する逆向きの力をカートに与えることができるかを考えてみます。
比例制御では，モータ指令値\(y_{tmp}\) は現在位置\(x\) によって定まり，
$$y_{tmp}=-k_p (x-r)$$ で生成されました。これは\(x-r\) に比例するような力をイメージしていると考えられます。
速度に比例する逆向きの力を加えたイメージで，モータ指令値\(y_{tmp}\) を作ることにすると次の式になります。
$$y_{tmp}=-k_p (x-r)-k_v v$$ この式で\(x-r\) に比例するような指令値と，\(v\)に比例するような逆向きの指令値の両方を発生することになります。

３　比例微分制御

「２ カートの振動をはやく減衰させる」で考えた
$$y_{tmp}=-k_p (x-r)-k_v v$$ を実現するには，速度の情報が必要です。
距離センサは現在位置しか測定できませんが，短い時間間隔\(T\)で現在位置を取得しています。時間\(T\)に進んだ距離から速度を求めることにします。
速度\(v\)は
$$v=\dfrac {x-x_{prev}} {T}$$ で求めることにします。
\(x\)は現在のカートの位置で，\(x_{prev}\)は現在より時間\(T\)前のカートの位置です。
（カートの速度も右向きが正の方向になります。\(0<x-x_{prev}\) なら右に向かって進んでいることになります。）

１つの式にまとめると
\(y_{tmp}=-k_p (x-r)-k_v \dfrac {x-x_{prev}} {T}=-k_p (x-r)- \dfrac {k_v}{T}(x-x_{prev})\)
になるので，\(\frac {k_v}{T}=k_d\)とおくと，
$$y_{tmp}=-k_p (x-r)-k_d (x-x_{prev})$$ となり，これが求める制御則になります。
実際のモータドライバの仕様により，モータ指令値の絶対値は100を超えることはできません。
モータに加える電圧が電源電圧を越えることができないのと同じです。
そこで\(y_{tmp}\)の絶対値が100を超えたところを100までに抑え込んでモータ指令値\(y\)とします。
$$y=\left \{ \begin{array}{cr} -100 & (y_{tmp}<-100) \\ y_{tmp} & (-100\leqq y_{tmp}<100) \\ 100 & (100\leqq y_{tmp}) \\ \end{array}\right.$$ フィードバック係数が２つ出てきましたが，区別して，\(k_p\)は位置フィードバック係数，\(k_d\)は速度フィードバック係数と呼ばれます。
速度は位置の時間微分なので，比例制御と合わせて比例微分制御と呼ばれます。微分はDifferentialなので，PD制御とも呼ばれます。

micro:bitで制御されたカートでの実験
比例微分制御では，位置フィードバック係数\(k_p\)と速度フィードバック\(k_d\)によって，カートの走行の様子が変化します。
2つのフィードバック係数の組み合わせは非常に多くなります。そこで \(k_p\)を0.8に固定し，\(k_d\)を0.2，0.4，0.8，1.6，2.0，3.0と変化させて，実験しています。目標位置\(r\)は-500mmです。
\(k_p=0.8\)というのは，比例制御のときに目標位置にははやく到達しますが，振動がなかなか止まらないというふるまいをしていました。

フィードバック係数\(k_d\)が小さな時ほど，振動を減衰させる作用が小さく，大きくすると振動を減衰させる作用が大きくなります
。 目標停止位置を少し超えて戻ってきて目標停止位置付近で停止するくらいの制御がもっともはやい目標停止位置到達になるとされています。
それ以上フィードバック係数\(k_d\)を大きくすると，振動しなくなり，ゆっくりと目標停止位置に停止するようになるはずですが，現実は複雑でそうはならず，停止直前に小さな振動を起こして，目標停止位置に到達できないといったことが起こります。

うまく制御できた時は数mmの精度で目標停止位置に停止します。

ここで使用している速度フィードバック係数\(k_d\)は速度を「80msecの時間に進んだ距離[mm]」しているときのものです。もし，測定間隔や長さの単位を変更した場合には場合には異なる値になります。

(1) フィードバック係数 \(k_p=0.8 \ k_v=0.2\) のとき
(A) カート位置のグラフ

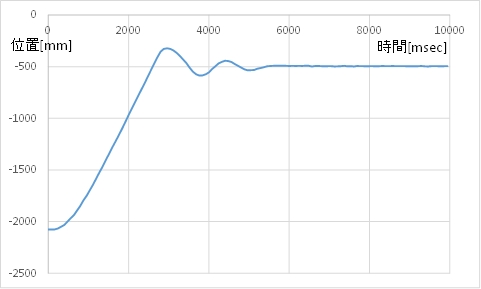
(B) モータ指令値（茶）とカートの速度（青）

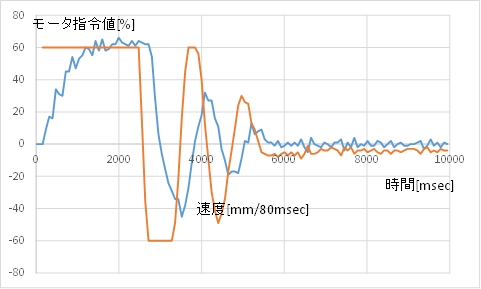
(C) 動画例　大きく行き過ぎて振動し，なかなか止まりません。
しかし停止位置の誤差は10mm未満になります。


(2) フィードバック係数 \(k_p=0.8 \ k_v=0.4\) のとき
(A) カート位置のグラフ

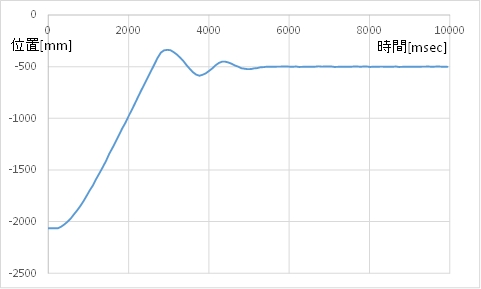
(B) モータ指令値（茶）とカートの速度（青）

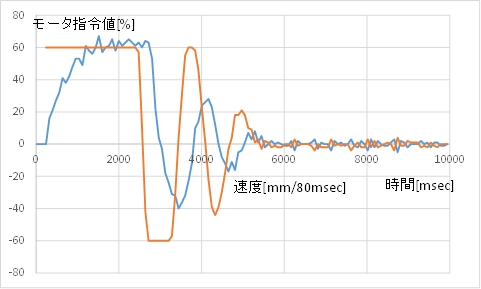
(C) 動画例　振動はまだ大きく，なかなか止まりません。
しかし停止位置の誤差は10mm未満になります。


(3) フィードバック係数 \(k_p=0.8 \ k_v=0.8\) のとき
(A) カート位置のグラフ

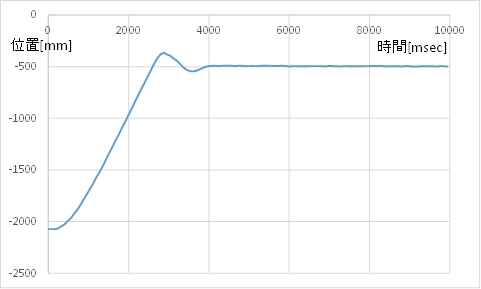
(B) モータ指令値（茶）とカートの速度（青）

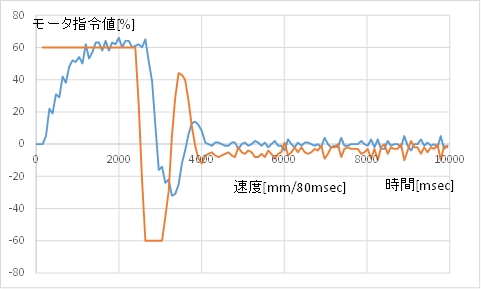
(C) 動画例　目標値に吸い寄せられる感じが出てきました。
停止位置の誤差は10mm未満になります。


(4) フィードバック係数 \(k_p=0.8 \ k_v=1.6\) のとき
(A) カート位置のグラフ

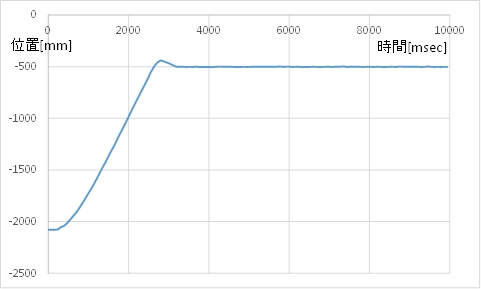
(B) モータ指令値（茶）とカートの速度（青）

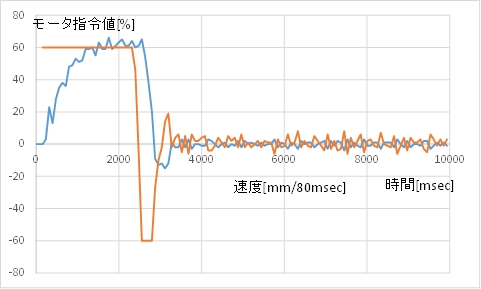
(C) 動画例　目標値に吸い寄せられる感じがします。
振動しており，まだ減衰は弱いです。
停止位置の誤差は10mm未満になります。


(5) フィードバック係数 \(k_p=0.8 \ k_v=2.0\) のとき
(A) カート位置のグラフ

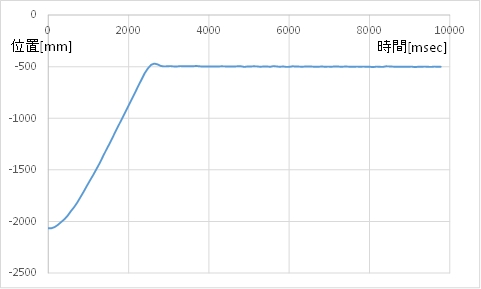
(B) モータ指令値（茶）とカートの速度（青）

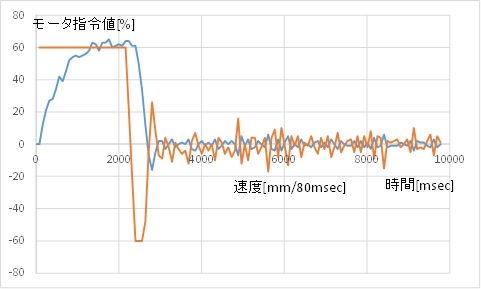
(C) 動画例　少しだけ行き過ぎてから戻り，そのまま目標位置で止まります。
停止位置の誤差は10mm未満になります。


(6) フィードバック係数 \(k_p=0.8 \ k_v=3.0\) のとき
(A) カート位置のグラフ

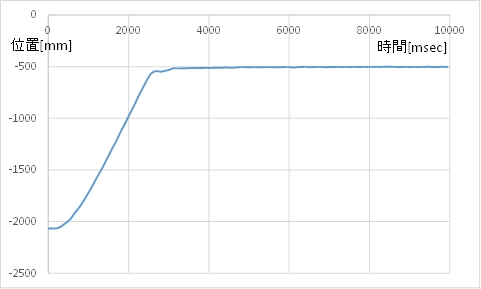
(B) モータ指令値（茶）とカートの速度（青）

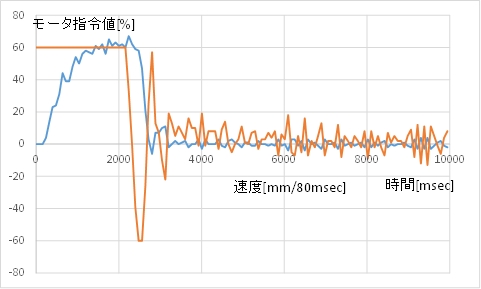
(C) 動画例　行き過ぎずに目標位置に止まります。
停止位置の誤差は10mm未満になります。

４　制御則とフィードバック係数の意味

\(y_{tmp}=-k_p (x-r)-k_d (x-x_{prev} )\) はイメージのとらえにくい式ですが，次のように考えると，意味が分かると思います。
(1)速度が0のとき（目標位置を中心とした往復動作という振動の両端では速度0になります）
\(x-x_{prev}=0\) になるので，
\(y_{tmp}=-k_p (x-r)\)
のみとなり，これはすでに出てきた比例制御と同じになります。
(2)カートが目標位置にいるとき
\(x-r=0\) になるので
\(y_{tmp}=-k_d (x-x_{prev} )\)
となります。
(2.1) カートが目標位置にいるが，右向きに速度を持っているとき
右向きの速度だから \(0<v\) なので，\(0<x-x_{prev}\) であり，\(y_{tmp}=-k_d (x-x_{prev} )<0\) になります。これは左向きのモータ指令値を与えることになり，カートの進行方向と逆のモータ指令値です。すなわち運動を止めようとします。
(2.2) カートが目標位置にいるが，左向きに速度を持っているとき
左向きの速度だから \(v<0\) なので，\(x-x_{prev}<0\) であり，\(y_{tmp}=-k_d (x-x_{prev} )>0\) になります。これは右向きのモータ指令値を与えることになり，カートの進行方向と逆のモータ指令値です。すなわち運動を止めようとします。

比例微分制御の制御則で振動を減衰させる様子がわかったと思います。
ところで\(k_p\)，\(k_d\)はどのように決めるのかという疑問がわきます。
\(k_p\)と\(k_d\)は，実験をしながらうまく制御できる値を探して決めるのが現実的です。
最初は速度フィードバック係数\(k_d=0\)としておいて，目標位置に速くたどり着くけれど振動が激しい動作になるという位置フィードバック係数\(k_p\)を求めます。
次に求められた\(k_p\)を固定して，\(k_d\)の値を徐々に大きくして，早く目標位置について，振動も少なくなる\(k_d\)を求めます。
このようにして求められた\(k_p\)と\(k_d\)をそれぞれ少しずつ変化させさらによい動きをするとことを探します。

５　まとめ

カートの制御（位置決め制御）について，素朴な考えからフィードバック制御まで解説しました。また振動抑制のための速度フィードバックに関しても概略を解説しました。

ここでは，カートを目的の位置に止めるという制御を例にとって考えましたが，その極意は，「目標位置の手前では前に進め，行き過ぎたら後ろに進め，しかもモータへの指令値の絶対値は目標位置から離れた距離に比例させなさい」という制御則です。（座標系によって数式での表現は異なりますが，言葉での表現は同一になります）
速度によるフィードバックに関しても「速度を持っていたら速度と反対方向に向けたモータ指令値を使いなさい。モータ指令値の絶対値は「速度の絶対値」に比例させなさい。」となっています。

この資料においては，位置決め制御を行いましたが，他の物理量を制御する場合でも共通することの多い内容です。ただし，場合によっては原理的に誤差0にならない（定常偏差）ことがあって，積分制御を導入することもあります。
その場合，制御系が不安定にならないように気を付ける必要があります。
これらの問題は，制御工学で学んでください。
この資料を読んだ後で制御工学を学ぶと，理解が容易になると思います。

リンク

(0)表紙ページ　フィードバック制御はじめの一歩	≫
(1)ある位置に到達したらモータを止める	≫
(2)目標位置前なら前進，行き過ぎたら後退	≫
（比例制御） (3)目標までの距離に比例したモータ指令値を作る	≫
（比例微分制御） (4)目標までの距離と速度からモータ指令値を作る（このページ）	≫